Integrable system
A differential system of dimension  (cf. Involutive distribution) on an
(cf. Involutive distribution) on an  -dimensional differentiable manifold
-dimensional differentiable manifold  that has, in a neighbourhood of each point
that has, in a neighbourhood of each point  , an
, an  -parameter family of
-parameter family of  -dimensional integral manifolds (cf. Integral manifold). One often speaks of a totally-integrable system in this case; more precisely it is defined as follows. Suppose that at each point
-dimensional integral manifolds (cf. Integral manifold). One often speaks of a totally-integrable system in this case; more precisely it is defined as follows. Suppose that at each point  a subspace
a subspace  of dimension
of dimension  in the tangent space
in the tangent space 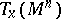 has been distinguished, such that a differential system, or distribution,
has been distinguished, such that a differential system, or distribution, 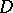 of class
of class 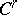 ,
, 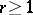 , of dimension
, of dimension 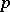 is given on
is given on  . The system
. The system  is called totally integrable if for each point
is called totally integrable if for each point  there is a coordinate system
there is a coordinate system 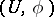 ,
,  ,
,  , such that for any constants
, such that for any constants 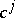 ,
,  , the manifold
, the manifold  is an integral submanifold, i.e. its tangent space at an arbitrary point coincides with
is an integral submanifold, i.e. its tangent space at an arbitrary point coincides with  . For analytic conditions that are necessary and sufficient for this, see Involutive distribution.
. For analytic conditions that are necessary and sufficient for this, see Involutive distribution.
Comments
Cf. also Pfaffian equation. The phrase integrable system is also used to refer to a completely-integrable Hamiltonian system or equation, i.e. a Hamiltonian equation (system) on a 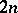 -dimensional phase space which has
-dimensional phase space which has  (including the Hamiltonian itself) integrals in involution, cf. Hamiltonian system.
(including the Hamiltonian itself) integrals in involution, cf. Hamiltonian system.
Integrable system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integrable_system&oldid=16009