Initial conditions

Conditions imposed in formulating the Cauchy problem for differential equations. For an ordinary differential equation in the form

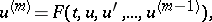(1)

the initial conditions prescribe the values of the derivatives (Cauchy data):

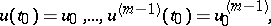(2)

where 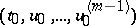is an arbitrary fixed point of the domain of definition of the function 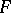; this point is known as the initial point of the required solution. The Cauchy problem (1), (2) is often called an initial value problem.

For a partial differential equation, written in normal form with respect to a distinguished variable ,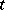

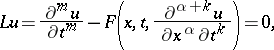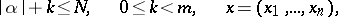the initial conditions consist in prescribing the values of the derivatives (Cauchy data)

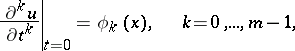of the required solution 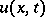on the hyperplane 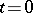(the support of the initial conditions).

References

[a1]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956)
[a2]	S. Mizohata, "The theory of partial differential equations" , Cambridge Univ. Press (1973) (Translated from Japanese)