Information, transmission of
The part of information theory related to the study of processes of information transfer from a source to a receiver (the addressee), cf. Information, source of. In the theory of information transmission one studies optimum and near-optimum methods of information transmission over a communication channel under the assumption that the methods of encoding the message into the input signal of the channel and of decoding the output signal of the channel into an output message may vary within wide ranges (cf. Coding and decoding).
The general scheme of systems of information transmission, first considered by C. Shannon [1], can be described as follows. The source of information produces the message that has to be transmitted over the communication channel from the source to the receiver. It is usually assumed that this message is a random variable defined on some probability space 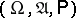 , taking values in a measurable space
, taking values in a measurable space 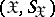 and having a probability distribution
and having a probability distribution 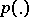 . Often
. Often 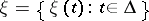 , where
, where 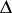 is the set of parameter values of
is the set of parameter values of 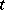 , is a stochastic process in discrete or continuous time and with values in a measurable space
, is a stochastic process in discrete or continuous time and with values in a measurable space 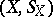 . E.g., in the case of discrete time
. E.g., in the case of discrete time 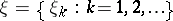 or
or 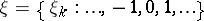 ; the random variables
; the random variables 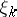 , taking values in
, taking values in 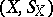 , are called the components of the input message and are often treated as the messages produced by the source at the moment of time
, are called the components of the input message and are often treated as the messages produced by the source at the moment of time 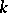 . The sets
. The sets 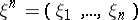 , taking values in the
, taking values in the  -fold product of
-fold product of 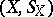 ,
, 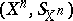 , are called segments of length
, are called segments of length  of the input message. The corresponding concepts are defined in an analogous way for the case of a continuous-time stochastic process as message.
of the input message. The corresponding concepts are defined in an analogous way for the case of a continuous-time stochastic process as message.
The output message, received by the receiver, is also a random variable 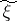 , defined on the same probability space
, defined on the same probability space 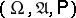 and taking values in a measurable space
and taking values in a measurable space 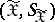 (in general, different from
(in general, different from 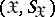 ). When
). When 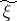 is a stochastic process in discrete or continuous time one introduces in an analogous way the concepts of the space
is a stochastic process in discrete or continuous time one introduces in an analogous way the concepts of the space 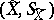 of values of the components at the output, and the space
of values of the components at the output, and the space 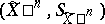 of values of the segments of length
of values of the segments of length  of the output message.
of the output message.
The exactness of reproducibility of information is taken as the measure for the quality of the transmission of the message over the communication channel (cf. Information, exactness of reproducibility of). As a rule, if the transmission is over a communication channel with noise, even if the sets 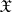 and
and 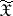 coincide, it is impossible to obtain absolute exactness, i.e. complete coincidence of the messages sent and received. Often, the requirement reflecting the exactness is treated statistically, by introducing the class
coincide, it is impossible to obtain absolute exactness, i.e. complete coincidence of the messages sent and received. Often, the requirement reflecting the exactness is treated statistically, by introducing the class 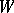 of admissible joint probability distributions for pairs
of admissible joint probability distributions for pairs 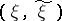 of messages sent and received in the set of all probability measures on the product
of messages sent and received in the set of all probability measures on the product 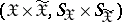 . The class
. The class 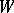 is often given by means of a non-negative measurable function
is often given by means of a non-negative measurable function 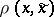 ,
, 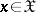 ,
, 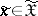 , and a number
, and a number 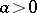 : It is considered that a probability distribution of
: It is considered that a probability distribution of 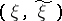 belongs to
belongs to 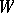 only if
only if
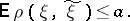 | (1) |
Thus, the condition of exactness of reproducibility indicates by what amount the message received can differ from the message sent.
Messages produced by a source are sent over a communication channel. A channel 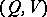 is a set of two measurable spaces
is a set of two measurable spaces 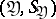 ,
, 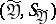 ; a transition function
; a transition function 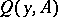 ,
, 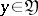 ,
, 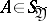 , that is measurable with respect to the
, that is measurable with respect to the 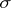 -algebra
-algebra 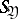 for fixed
for fixed 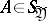 and is a probability measure on
and is a probability measure on 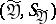 for fixed
for fixed 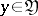 ; and a subset
; and a subset 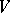 in the space of all probability measures on
in the space of all probability measures on 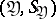 . The spaces
. The spaces 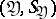 ,
, 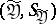 are called, respectively, the spaces of input and output signals of the channel, and
are called, respectively, the spaces of input and output signals of the channel, and 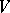 is a restriction on the distribution of the input signal. One says that two random variables
is a restriction on the distribution of the input signal. One says that two random variables 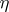 and
and 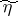 (defined on a probability space
(defined on a probability space 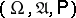 ) are related through a channel
) are related through a channel 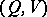 if they take values in
if they take values in 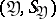 and
and 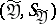 , respectively, and if for any
, respectively, and if for any 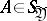 with probability 1 the conditional probability
with probability 1 the conditional probability
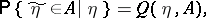 | (2) |
and the probability distribution of 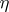 belongs to
belongs to 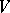 . Most often
. Most often 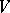 is given by a measurable function
is given by a measurable function 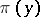 ,
, 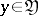 , and a number
, and a number 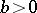 : It is considered that the probability distribution of
: It is considered that the probability distribution of 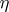 belongs to
belongs to 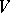 only if
only if
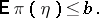 | (3) |
In the case of discrete channels 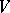 usually coincides with the set of all probability distributions, i.e. there is no restriction.
usually coincides with the set of all probability distributions, i.e. there is no restriction.
In fact, 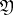 is the set of signals given by the transmitter, and
is the set of signals given by the transmitter, and 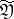 is the set of signals taken by the receiver (in applications
is the set of signals taken by the receiver (in applications 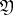 and
and  often coincide). If the random variable
often coincide). If the random variable 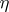 of the input signal is known, then (2) makes it possible to find the conditional distribution of the output signal
of the input signal is known, then (2) makes it possible to find the conditional distribution of the output signal 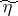 . The introduction of the restriction
. The introduction of the restriction 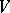 is related to the fact that in many applications the distributions of the input signal cannot be taken arbitrarily (the case when it is supposed that the mean value of the square (the power) of the input signal does not exceed a fixed constant is typical). The case when the input and output signals are discrete- or continuous-time stochastic processes
is related to the fact that in many applications the distributions of the input signal cannot be taken arbitrarily (the case when it is supposed that the mean value of the square (the power) of the input signal does not exceed a fixed constant is typical). The case when the input and output signals are discrete- or continuous-time stochastic processes 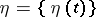 ,
, 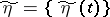 defined on a certain finite or infinite (at one or both sides) interval on the real axis and taking values in certain measurable spaces
defined on a certain finite or infinite (at one or both sides) interval on the real axis and taking values in certain measurable spaces  and
and 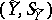 , respectively, is important in applications. E.g., if
, respectively, is important in applications. E.g., if 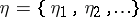 and
and 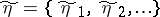 are random sequences, then the communication channel for which
are random sequences, then the communication channel for which 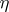 and
and 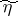 serve as input and output signals is often regarded as a sequence of channels (in the sense described above), called segments of the given channel; the input and output signals of these segments are the vectors
serve as input and output signals is often regarded as a sequence of channels (in the sense described above), called segments of the given channel; the input and output signals of these segments are the vectors
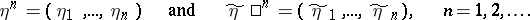 |
In order to convert the input message into a signal transmittable over the communication channel and the signal received at the output of the channel into an output message it is necessary to perform operations of encoding and decoding of messages. An encoding is a function 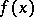 of
of 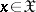 with values in
with values in 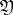 , and a decoding is a function
, and a decoding is a function 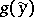 of
of 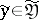 with values in
with values in 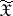 . The set of values of
. The set of values of 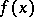 ,
, 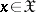 , is called a code, and the individual elements of this set are called code words. Using an encoding
, is called a code, and the individual elements of this set are called code words. Using an encoding 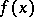 and a decoding
and a decoding 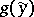 means that if the message took the value
means that if the message took the value 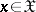 , then one transmits
, then one transmits 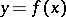 over the channel; if
over the channel; if 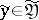 is received at the output of the channel, then it is decoded into the output message
is received at the output of the channel, then it is decoded into the output message 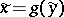 . One often considers random encodings in the theory of information transmission, i.e. the code words are chosen randomly in correspondence with a certain probability distribution.
. One often considers random encodings in the theory of information transmission, i.e. the code words are chosen randomly in correspondence with a certain probability distribution.
A message with probability distribution 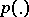 , produced by the source, can be transmitted with exactness of reproducibility
, produced by the source, can be transmitted with exactness of reproducibility 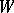 over a channel
over a channel 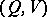 by means of an encoding
by means of an encoding 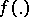 and a decoding
and a decoding 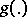 if random variables
if random variables 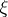 ,
, 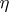 ,
, 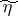 ,
, 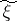 forming a Markov chain can be constructed such that
forming a Markov chain can be constructed such that 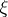 has probability distribution
has probability distribution 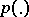 , the probability distribution of
, the probability distribution of 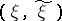 belongs to
belongs to 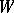 , the pair
, the pair 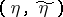 is related through
is related through 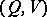 , and
, and
 | (4) |
The assumption that 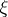 ,
, 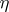 ,
, 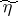 ,
, 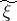 form a Markov chain reduces to the assumption that the conditional probability of
form a Markov chain reduces to the assumption that the conditional probability of 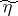 for fixed values of
for fixed values of 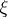 and
and 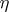 depends on
depends on 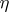 only, i.e. it means that the output signal depends only on the input signal and not on the value of the message encoded by it.
only, i.e. it means that the output signal depends only on the input signal and not on the value of the message encoded by it.
The basic problem studied in the transmission of information is as follows. One considers known and fixed: a source generating messages with probability densities 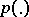 ; a communication channel
; a communication channel 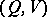 ; and a condition of exactness of reproducibility
; and a condition of exactness of reproducibility 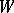 . The problem is to clarify: Under what conditions does there exist an encoding
. The problem is to clarify: Under what conditions does there exist an encoding 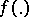 and a decoding
and a decoding 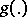 such that a message produced by the given source can be transmitted with given
such that a message produced by the given source can be transmitted with given 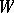 over
over 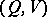 ? Solutions to this problem for various assumptions are called coding theorems, or Shannon theorems. Another naturally arising problem is that when transmittance is possible, to construct the most simple and efficient ways of encoding and decoding the transmission.
? Solutions to this problem for various assumptions are called coding theorems, or Shannon theorems. Another naturally arising problem is that when transmittance is possible, to construct the most simple and efficient ways of encoding and decoding the transmission.
Shannon [1] introduced quantities that allow one to formulate an answer to the first problem posed. The amount of information, or simply the information, 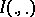 is the most important among these (cf. Information, amount of). If
is the most important among these (cf. Information, amount of). If
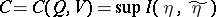 |
is the capacity of the channel 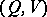 (cf. Transmission rate of a channel), where the supremum is over all pairs
(cf. Transmission rate of a channel), where the supremum is over all pairs 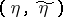 related through
related through 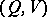 , and if the number
, and if the number
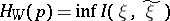 | (6) |
is the 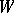 -entropy (cf. Entropy) of the message, where the infimum is over all pairs
-entropy (cf. Entropy) of the message, where the infimum is over all pairs 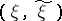 such that the joint probability distribution of
such that the joint probability distribution of 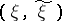 belongs to
belongs to 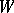 , while
, while 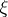 has probability distribution
has probability distribution 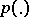 , then the following theorem of Shannon (a converse of coding theorems) holds: If a message with probability distribution
, then the following theorem of Shannon (a converse of coding theorems) holds: If a message with probability distribution 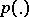 can be transmitted over
can be transmitted over 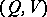 with exactness of reproducibility
with exactness of reproducibility 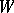 , then
, then
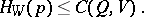 | (7) |
Sufficient conditions for the possibility of transmission of information are more difficult to obtain. Thus, (7) is sufficient only in a certain asymptotic sense, in which the main assumption is that 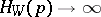 . Hence, (7) is necessary and sufficient only, roughly speaking, when applied to the problem of transmitting a sufficiently large amount of information. The remaining necessary assumptions are of the nature of regularity assumptions, which in concrete cases are usually fulfilled. In order to formulate sufficient conditions for the possibility of transmission in exact terms it is necessary to introduce supplementary concepts.
. Hence, (7) is necessary and sufficient only, roughly speaking, when applied to the problem of transmitting a sufficiently large amount of information. The remaining necessary assumptions are of the nature of regularity assumptions, which in concrete cases are usually fulfilled. In order to formulate sufficient conditions for the possibility of transmission in exact terms it is necessary to introduce supplementary concepts.
A sequence of pairs of random variables 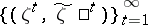 is called information-stable if
is called information-stable if 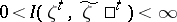 and
and
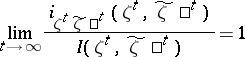 | (8) |
in the sense of convergence in probability. Here 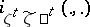 is the information density (cf. Information, amount of) of
is the information density (cf. Information, amount of) of 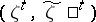 . A sequence of channels
. A sequence of channels 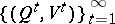 with
with 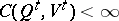 is called information-stable if there exists an information-stable sequence of pairs
is called information-stable if there exists an information-stable sequence of pairs 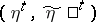 , related through
, related through 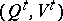 , such that
, such that
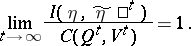 | (9) |
A sequence of messages with probability distributions 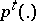 and exactness conditions
and exactness conditions 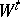 with
with 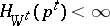 ,
, 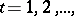 is called information-stable if there exists a sequence of pairs
is called information-stable if there exists a sequence of pairs 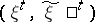 such that
such that 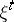 has probability density
has probability density 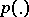 , the probability distribution of
, the probability distribution of 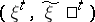 belongs to
belongs to 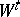 , and
, and
 | (10) |
Let 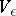 be the set of probability distributions for which (3) with
be the set of probability distributions for which (3) with  replaced by
replaced by 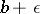 holds, and let
holds, and let 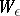 be the exactness condition given by (1) with
be the exactness condition given by (1) with  replaced by
replaced by 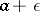 ,
, 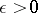 . The following coding theorem (Shannon) holds: Suppose one is given an information-stable sequence of messages with probability densities
. The following coding theorem (Shannon) holds: Suppose one is given an information-stable sequence of messages with probability densities 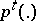 and exactness conditions
and exactness conditions 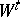 , as well as an information-stable sequence of channels
, as well as an information-stable sequence of channels  such that the functions
such that the functions  and
and 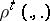 are uniformly bounded in
are uniformly bounded in 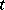 . Let
. Let 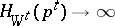 as
as 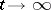 and let
and let
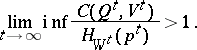 | (11) |
Then for any  there exists an arbitrary large
there exists an arbitrary large  such that for all
such that for all 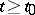 the messages with probability distributions
the messages with probability distributions 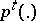 can be transmitted over
can be transmitted over 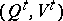 with exactness of reproducibility
with exactness of reproducibility 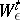 .
.
This formulation of a direct coding theorem is most general. The assumption that 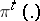 and
and 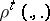 are uniformly bounded in
are uniformly bounded in 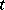 can be substantially weakened. The information stability of a sequence of messages or channels is true in a large number of particular cases of practical interest. Finally, under certain conditions one may replace
can be substantially weakened. The information stability of a sequence of messages or channels is true in a large number of particular cases of practical interest. Finally, under certain conditions one may replace 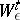 by
by 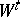 and
and 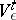 by
by 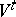 in the formulation of the theorem.
in the formulation of the theorem.
In the description of real situations the case when the sequence of channels considered in the theorem is the sequence of segments of a fixed channel, while the sequence of messages is the sequence of segments of a message from a fixed source with growing number of components is of most interest. This corresponds to the functioning of a communication system in time. Below some versions of the coding theorem and its converse are given for this situation, in a somewhat different form. Moreover, discrete stationary sources and memoryless communication channels are considered.
Suppose that a discrete stationary source 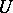 produces messages
produces messages 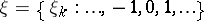 , where the individual components (the letters of the message)
, where the individual components (the letters of the message) 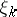 take values from some finite set of an alphabet
take values from some finite set of an alphabet 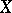 of volume
of volume 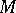 , and generates letters of messages at the rate of one letter per unit of time. Let the components of the message
, and generates letters of messages at the rate of one letter per unit of time. Let the components of the message 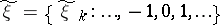 received by the addressee take values in the same alphabet
received by the addressee take values in the same alphabet 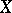 (i.e.
(i.e. 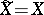 ). Suppose further that a discrete memoryless channel is being used, and that transmission over it is at the rate of one symbol per time interval
). Suppose further that a discrete memoryless channel is being used, and that transmission over it is at the rate of one symbol per time interval  . Suppose that there are no restrictions on the distribution of the input signal of the channel. Suppose that a segment of length
. Suppose that there are no restrictions on the distribution of the input signal of the channel. Suppose that a segment of length 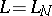 of a message,
of a message, 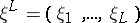 , is transmitted over the channel by intervals of length
, is transmitted over the channel by intervals of length 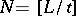 (where
(where  is the integer part of a number
is the integer part of a number  ) using certain encoding and decoding methods of the type described above. Then if
) using certain encoding and decoding methods of the type described above. Then if 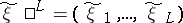 is the corresponding segment of the message obtained by the addressee and
is the corresponding segment of the message obtained by the addressee and 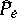 is the average probability of an error in a source letter, defined by
is the average probability of an error in a source letter, defined by
 | (12) |
then the following theorem holds.
Converse of the coding theorem: Let 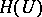 be the rate of creation of messages of the given discrete stationary source and let
be the rate of creation of messages of the given discrete stationary source and let 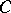 be the transmission rate (on transmitted symbols) of the memoryless channel used. Then for all
be the transmission rate (on transmitted symbols) of the memoryless channel used. Then for all 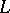 :
:
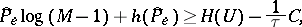 | (13) |
where
 |
Thus, if the rate of creation of messages  is larger than
is larger than 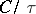 (the transmission rate of the channel on a source letter), then the average probability of an error in a source letter is bounded from below by a non-zero constant, whatever
(the transmission rate of the channel on a source letter), then the average probability of an error in a source letter is bounded from below by a non-zero constant, whatever 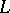 and the methods of encoding and decoding. Hence, this probability does not tend to zero as
and the methods of encoding and decoding. Hence, this probability does not tend to zero as 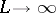 .
.
In order to formulate the direct statement of a coding theorem one needs the quantity
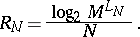 | (14) |
When 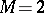 and
and 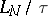 is an integer one has
is an integer one has  , i.e.
, i.e. 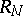 is in bits (cf. Bit) the number of binary symbols produced by the source within the transmission time of one symbol over the channel. Moreover,
is in bits (cf. Bit) the number of binary symbols produced by the source within the transmission time of one symbol over the channel. Moreover, 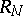 coincides with
coincides with 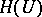 if the components are independent and identically distributed. The probability of an error and the average probability of an error in a block of the source are defined respectively, by,
if the components are independent and identically distributed. The probability of an error and the average probability of an error in a block of the source are defined respectively, by,
 | (15) |
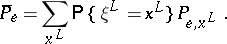 | (16) |
Here 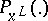 is the conditional probability under the condition
is the conditional probability under the condition 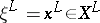 . The following coding theorem holds: For all
. The following coding theorem holds: For all 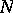 and any
and any 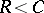 there are encoding and decoding methods such that for
there are encoding and decoding methods such that for 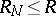 and all
and all 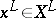 ,
,
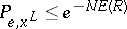 | (17) |
(this also holds for 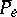 ). Moreover, for
). Moreover, for 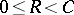 the function
the function 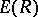 is convex, positive and decreases with increasing
is convex, positive and decreases with increasing 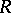 (see also Erroneous decoding, probability of). Thus, this theorem also shows that for all
(see also Erroneous decoding, probability of). Thus, this theorem also shows that for all 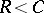 the probability of an error tends to zero, exponentially fast, as
the probability of an error tends to zero, exponentially fast, as 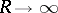 .
.
There are generalizations of Shannon theorems to the cases of so-called compound channels and messages with independent parameters. Such generalizations are of interest because in practice it is impossible to regard the statistical parameters of the source of messages and the communication channel as completely known, since these parameters can sometimes change in the process of transmission. Therefore, it is appropriate to assure that the source of the messages and the communication channel belong to a certain class of possible sources and channels. One introduces, moreover, the minimax criterion for the quality of transmission, in which the quality of a given transmission method is estimated for the best possible sources and channels belonging to the given classes.
There are also generalizations of Shannon theorems to the transmission of information over a channel with feedback. The presence of complete feedback means that at the moment of time  it is considered that at the transmitting side of the channel (i.e. at its input) all exact values of the output signals at all moments
it is considered that at the transmitting side of the channel (i.e. at its input) all exact values of the output signals at all moments 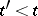 are known. In particular, for a memoryless channel with feedback the basic result is that the presence of feedback does not increase the transmission rate of the channel, although it may substantially decrease the complexity of the encoding and decoding devices.
are known. In particular, for a memoryless channel with feedback the basic result is that the presence of feedback does not increase the transmission rate of the channel, although it may substantially decrease the complexity of the encoding and decoding devices.
Other generalizations to be mentioned are the theory of information transmission over channels with error synchronization, in which random synchronizations are possible, with as result the disturbance of the one-to-one correspondence between the input and output signal, as well as the theory of transmission over a channel with multiple directions, when there are several sources and receivers of information, and where transmission may proceed over several directions at the same time.
References
| [1] | C. Shannon, "A mathematical theory of communication" Bell Systems Techn. J. , 27 (1948) pp. 379–423; 623–656 |
| [2] | P.L. Dobrushin, "A general formulation of the fundamental theorem of Shannon in information theory" Uspekhi Mat. Nauk , 14 : 4 (1959) pp. 3–104 (In Russian) |
| [3] | J. Wolfowitz, "Coding theorems of information theory" , Springer (1964) |
| [4] | R. Gallager, "Theory of information and reliable communication" , Wiley (1968) |
| [5] | A.A. Feinstein, "Foundations of information theory" , McGraw-Hill (1968) |
| [6] | R.M. Fano, "Transmission of information. Statistical theory of communications" , M.I.T. (1963) |
| [7] | A.A. Kharkevich, "Channels with noise" , Moscow (1965) (In Russian) |
| [8] | J.M. Wozencraft, I.M. Jacobs, "Principles of communication engineering" , Wiley (1965) |
| [9] | A.N. Kolmogorov, "Three approaches to the definition of the concept of "amount of information" " Probl. Peredachi Inform. , 1 : 1 (1965) pp. 3–11 (In Russian) |
| [10] | M.S. Pinsker, "Information and informational stability of random variables and processes" , Holden-Day (1964) (Translated from Russian) |
| [11] | B.R. Levin, "Theoretical foundations of statistical radiotechnics" , Moscow (1974) (In Russian) |
| [12] | A.N. Kolmogorov, "The theory of information transmission" , Meeting of the USSR Acad. Sci. on Scientific Problems of Automatizing Society 15–20 Oct. 1956, Talin. , 1 , Moscow (1957) pp. 66–99 (In Russian) |
| [13] | D. Slepian (ed.) , Key papers in the development of information theory , IEEE (1974) |
| [14] | , Proc. 1975 IEEE-USSR Joint Workshop Inform. Theory (Moscow, 15–19 Dec. 1975) , IEEE (1976) |
Information, transmission of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Information,_transmission_of&oldid=11654