Information, rate of generation of
A quantity characterizing the amount of information (cf. Information, amount of) emanating from an information source in unit time. The rate of generation of information of an information source  with discrete time generating the communication
with discrete time generating the communication 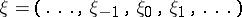 , formed by a sequence of random variables
, formed by a sequence of random variables  taking values from some discrete set
taking values from some discrete set 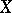 , is defined by the equation
, is defined by the equation
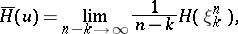 | (*) |
if this limit exists. Here 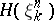 is the entropy of the random variable
is the entropy of the random variable 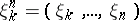 . The variable
. The variable 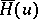 , defined by (*), is also called the entropy (in a symbol) of the information source.
, defined by (*), is also called the entropy (in a symbol) of the information source.
In certain cases one can successfully prove the existence of the limit in (*) and calculate it explicitly, e.g. in the case of stationary sources. Explicit formulas for 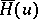 have been obtained for stationary Markov sources and Gaussian sources. The concept of a rate of generation of information is closely related to that of redundancy of an information source.
have been obtained for stationary Markov sources and Gaussian sources. The concept of a rate of generation of information is closely related to that of redundancy of an information source.
If  is a stationary ergodic information source with finite number of states, then the following property of asymptotic uniform distribution (the McMillan theorem, [1]) holds. Let
is a stationary ergodic information source with finite number of states, then the following property of asymptotic uniform distribution (the McMillan theorem, [1]) holds. Let 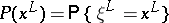 , where
, where 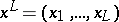 are the values of
are the values of  in an information interval of length
in an information interval of length 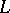 . For any
. For any 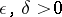 , there is an
, there is an 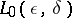 such that for all
such that for all 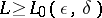 ,
,
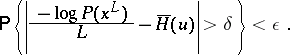 |
References
| [1] | J. Wolfowitz, "Coding theorems of information theory" , Springer (1961) |
| [2] | R. Gallagher, "Information theory and reliable communication" , Wiley (1968) |
| [3] | A.A. Feinstein, "Foundations of information theory" , McGraw-Hill (1958) |
Comments
References
| [a1] | I. Csiszar, J. Körner, "Information theory. Coding theorems for discrete memoryless systems" , Akad. Kiado (1981) |
| [a2] | A. Rényi, "A diary on information theory" , Akad. Kiado & Wiley (1987) |
Information, rate of generation of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Information,_rate_of_generation_of&oldid=15080