Information, amount of

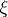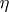An information-theoretical measure of the quantity of information contained in one random variable relative to another random variable. Let and be random variables defined on a probability space 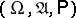and taking values in measurable spaces (cf. Measurable space) 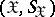and 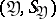, respectively. Let 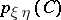, , 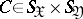and 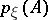, , 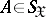, , 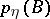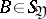be their joint and marginale probability distributions. If 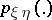is absolutely continuous with respect to the direct product of measures 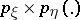, if 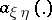is the (Radon–Nikodým) density of 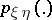with respect to 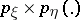, and if 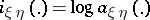is the information density (the logarithms are usually taken to base 2 or ), then, by definition, the amount of information is given by

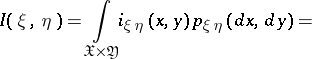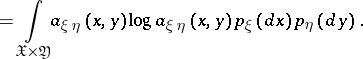If 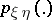is not absolutely continuous with respect to 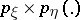, then 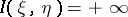, by definition.

In case the random variables 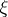and 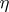take only a finite number of values, the expression for 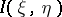takes the form

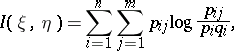where

are the probability functions of 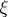, 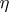and the pair 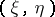, respectively. (In particular,

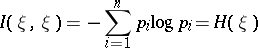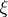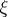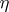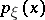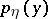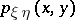is the entropy of .) In case and are random vectors and the densities , and of 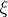, 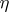and the pair 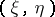, respectively, exist, one has

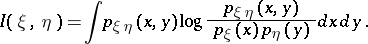In general,

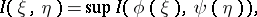where the supremum is over all measurable functions 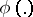and 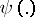with a finite number of values. The concept of the amount of information is mainly used in the theory of information transmission.

For references, see , ,

to Information, transmission of.