Difference between revisions of "Infinite game"
(Importing text file) |
Squinterodlr (talk | contribs) m (Changed an equation to TeX encoding.) |
||
| Line 1: | Line 1: | ||
A [[Non-cooperative game|non-cooperative game]], in particular a [[Two-person zero-sum game|two-person zero-sum game]], with infinite sets of player strategies. Let | A [[Non-cooperative game|non-cooperative game]], in particular a [[Two-person zero-sum game|two-person zero-sum game]], with infinite sets of player strategies. Let | ||
| − | + | $$\Gamma = (X_1,X_2,...,X_n,H_1,H_2,...,H_n)$$ | |
be an infinite game with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508602.png" /> participants. It was shown by C. Berge [[#References|[1]]] that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508603.png" /> are locally convex compact linear topological Hausdorff spaces, if the pay-off functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508604.png" /> are continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508605.png" /> and are quasi-concave for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508606.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508607.png" />, then the game <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508608.png" /> has equilibrium points (solutions). It was also shown [[#References|[2]]] that if the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508609.png" /> are compact Hausdorff spaces and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i05086010.png" /> are continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i05086011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i05086012.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i05086013.png" /> has equilibrium points in mixed strategies. However, not all infinite games have equilibrium points, even in mixed strategies. For example, for the two-person zero-sum game in which the sets of player strategies are sets of integers, while the pay-off function has the form | be an infinite game with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508602.png" /> participants. It was shown by C. Berge [[#References|[1]]] that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508603.png" /> are locally convex compact linear topological Hausdorff spaces, if the pay-off functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508604.png" /> are continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508605.png" /> and are quasi-concave for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508606.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508607.png" />, then the game <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508608.png" /> has equilibrium points (solutions). It was also shown [[#References|[2]]] that if the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i0508609.png" /> are compact Hausdorff spaces and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i05086010.png" /> are continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i05086011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i05086012.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050860/i05086013.png" /> has equilibrium points in mixed strategies. However, not all infinite games have equilibrium points, even in mixed strategies. For example, for the two-person zero-sum game in which the sets of player strategies are sets of integers, while the pay-off function has the form | ||
Revision as of 23:06, 19 November 2012
A non-cooperative game, in particular a two-person zero-sum game, with infinite sets of player strategies. Let
$$\Gamma = (X_1,X_2,...,X_n,H_1,H_2,...,H_n)$$
be an infinite game with  participants. It was shown by C. Berge [1] that if
participants. It was shown by C. Berge [1] that if  are locally convex compact linear topological Hausdorff spaces, if the pay-off functions
are locally convex compact linear topological Hausdorff spaces, if the pay-off functions  are continuous on
are continuous on  and are quasi-concave for
and are quasi-concave for  ,
,  , then the game
, then the game  has equilibrium points (solutions). It was also shown [2] that if the
has equilibrium points (solutions). It was also shown [2] that if the  are compact Hausdorff spaces and the
are compact Hausdorff spaces and the 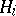 are continuous on
are continuous on 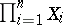 ,
,  , then
, then 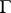 has equilibrium points in mixed strategies. However, not all infinite games have equilibrium points, even in mixed strategies. For example, for the two-person zero-sum game in which the sets of player strategies are sets of integers, while the pay-off function has the form
has equilibrium points in mixed strategies. However, not all infinite games have equilibrium points, even in mixed strategies. For example, for the two-person zero-sum game in which the sets of player strategies are sets of integers, while the pay-off function has the form
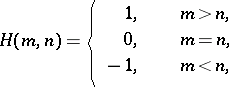 |
no value exists. The best studied classes of infinite games in normal form are infinite two-person zero-sum games and, in particular, games on the unit square (cf. Game on the unit square).
References
| [1] | C. Berge, "Théorie génerale des jeux à  personnes" , Gauthier-Villars (1957) personnes" , Gauthier-Villars (1957) |
| [2] | I.L. Gliksberg, "A further generalization of the Kakutani fixed point theorem with application to Nash equilibrium points" Proc. Amer. Math. Soc. , 3 : 1 (1952) pp. 170–174 |
Infinite game. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinite_game&oldid=28796