Inductive dimension
large inductive dimension 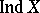 , small inductive dimension
, small inductive dimension 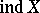
Dimension invariants (cf. Dimension invariant) of a topological space 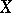 ; both are defined by means of the notion of a partition between two sets. The definition is by induction, as follows. For the empty space
; both are defined by means of the notion of a partition between two sets. The definition is by induction, as follows. For the empty space 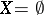 one sets
one sets 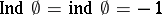 . Under the hypothesis that all spaces
. Under the hypothesis that all spaces 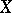 for which
for which 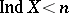 are known, where
are known, where  is a non-negative integer, one puts
is a non-negative integer, one puts 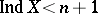 if for any two disjoint closed subsets
if for any two disjoint closed subsets 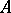 and
and 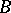 of
of 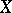 there is a partition
there is a partition 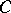 between them for which
between them for which 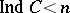 . Here, a closed set
. Here, a closed set 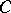 is called a partition between
is called a partition between 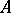 and
and 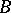 in
in 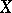 if the open set
if the open set  is the sum of two open disjoint sets
is the sum of two open disjoint sets 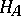 and
and 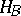 containing
containing 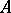 and
and 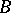 , respectively. This definition transfers to the definition of small inductive dimension
, respectively. This definition transfers to the definition of small inductive dimension 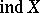 by taking one of the sets
by taking one of the sets 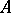 or
or 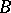 to consist of a single point, while the other is an arbitrary closed set not containing this point.
to consist of a single point, while the other is an arbitrary closed set not containing this point.
The large inductive dimension was defined for a fairly wide class of (metric) spaces by L.E.J. Brouwer [1]. The small inductive dimension was defined independently by P.S. Urysohn [2] and K. Menger [3]. The study of inductive dimensions and, more generally, of dimension invariants, is only of interest under the hypothesis that the space 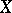 satisfies sufficiently strong separation axioms, mainly the axiom of normality (cf. Separation axiom).
satisfies sufficiently strong separation axioms, mainly the axiom of normality (cf. Separation axiom).
References
| [1] | L.E.J. Brouwer, "Ueber den natürlichen Dimensionsbegriff" J. Reine Angew. Math. , 142 (1913) pp. 146–152 |
| [2] | P.S. Urysohn, "Les multiplicités cantoriennes" C.R. Acad. Sci. , 175 (1922) pp. 440–442 |
| [3] | K. Menger, "Ueber die Dimensionalität von Punktmengen. I" Monatshefte Math. und Phys. , 33 (1923) pp. 148–160 |
| [4] | P.S. Aleksandrov, B.A. Pasynkov, "Introduction to dimension theory" , Moscow (1973) (In Russian) |
Comments
An extensive treatment of the subject can be found in [a1]. For a quick introduction to the dimension theory of separable metric spaces, see [a2], Chapt. 4.
References
| [a1] | R. Engelking, "Dimension theory" , North-Holland & PWN (1978) |
| [a2] | J. van Mill, "Infinite-dimensional topology, prerequisites and introduction" , North-Holland (1988) |
Inductive dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inductive_dimension&oldid=13316