Index theory
The area of mathematics whose main object of study is the index of operators (cf. also Index of an operator; Index formulas).
The main question in index theory is to provide index formulas for classes of Fredholm operators (cf. also Fredholm operator), but this is not the only interesting question. First of all, to be able to provide index formulas, one has to specify what meaning of "index" is agreed upon, then one has to specify to what classes of operators these formulas will apply, and, finally, one has to explain how to use these formulas in applications.
A consequence of this is that index theory also studies various generalizations of the concept of Fredholm index, including 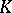 -theoretical and cyclic homology indices, for example. Moreover, the study of the analytic properties necessary for the index to be defined are an important part of index theory. Here one includes the study of conditions for being Fredholm or non-Fredholm for classes of operators that nevertheless have finite-dimensional kernels. Soon after (1970s), other invariants of elliptic operators have been defined that are similar in nature to the analytic index. The study of these related invariants is also commonly considered to be part of index theory. The most prominent of these new, related invariants are the Ray–Singer analytic torsion and the eta-invariant. Fixed-point formulas are also usually considered part of index theory, see [a9]. Finally, one of the most important goals of index theory is to study applications of the index theorems to geometry, physics, group representations, analysis, and other fields. There is a very long and fast growing list of papers dealing with these applications.
-theoretical and cyclic homology indices, for example. Moreover, the study of the analytic properties necessary for the index to be defined are an important part of index theory. Here one includes the study of conditions for being Fredholm or non-Fredholm for classes of operators that nevertheless have finite-dimensional kernels. Soon after (1970s), other invariants of elliptic operators have been defined that are similar in nature to the analytic index. The study of these related invariants is also commonly considered to be part of index theory. The most prominent of these new, related invariants are the Ray–Singer analytic torsion and the eta-invariant. Fixed-point formulas are also usually considered part of index theory, see [a9]. Finally, one of the most important goals of index theory is to study applications of the index theorems to geometry, physics, group representations, analysis, and other fields. There is a very long and fast growing list of papers dealing with these applications.
Index theory has become a subject on its own only after M.F. Atiyah and I. Singer published their index theorems in the sequence of papers [a4], [a6], [a7] (cf. also Index formulas). These theorems had become possible only due to progress in the related fields of 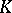 -theory [a10], [a5] and pseudo-differential operators (cf. also Pseudo-differential operator) [a35], [a37], [a46]. Important particular cases of the Atiyah–Singer index theorems were known before. Among them, Hirzebruch's signature theorem (cf. also Signature) occupies a special place (see [a33], especially for topics such as multiplicative genera and the Langlands formula for the dimension of spaces of automorphic forms). Hirzebruch's theorem was generalized by A. Grothendieck (see [a22]), who introduced many of the ideas that proved to be fundamental for the proof of the index theorems. All these theorems turned out to be consequences of the Atiyah–Singer index theorems (see also Index formulas for some index formulas that preceded the Atiyah–Singer index formula).
-theory [a10], [a5] and pseudo-differential operators (cf. also Pseudo-differential operator) [a35], [a37], [a46]. Important particular cases of the Atiyah–Singer index theorems were known before. Among them, Hirzebruch's signature theorem (cf. also Signature) occupies a special place (see [a33], especially for topics such as multiplicative genera and the Langlands formula for the dimension of spaces of automorphic forms). Hirzebruch's theorem was generalized by A. Grothendieck (see [a22]), who introduced many of the ideas that proved to be fundamental for the proof of the index theorems. All these theorems turned out to be consequences of the Atiyah–Singer index theorems (see also Index formulas for some index formulas that preceded the Atiyah–Singer index formula).
Atiyah–Singer index formulas.
A common characteristic of the first three main index formulas of Atiyah–Singer and Atiyah–Segal is that they depend only on the principal symbol of the operator whose index they compute. (For a differential operator, the principal symbol is given by the terms involving only the highest-order differentials and is independent of the choice of a coordinate system; cf. also Principal part of a differential operator; Symbol of an operator.) The main theorems mentioned above are:
the index theorem for a single elliptic operator 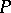 acting between sections of vector bundles on a smooth, compact manifold
acting between sections of vector bundles on a smooth, compact manifold 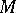 (Atiyah–Singer, [a4]);
(Atiyah–Singer, [a4]);
the equivariant index theorem for a single elliptic operator equivariant with respect to a compact group 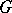 (Atiyah–Segal, [a5]); and
(Atiyah–Segal, [a5]); and
the index theorem for families 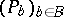 of elliptic operators acting on the fibres of a fibre bundle
of elliptic operators acting on the fibres of a fibre bundle 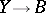 (Atiyah–Singer, [a7]). These results are briefly reviewed below.
(Atiyah–Singer, [a7]). These results are briefly reviewed below.
A single elliptic operator acting between sections of vector bundles.
If 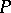 is an elliptic differential, or, more generally, an elliptic pseudo-differential operator acting between sections of two smooth vector bundles (cf. also Elliptic operator), then
is an elliptic differential, or, more generally, an elliptic pseudo-differential operator acting between sections of two smooth vector bundles (cf. also Elliptic operator), then 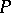 defines a continuous operator between suitable Sobolev spaces with closed range and finite-dimensional kernel and cokernel, that is, a Fredholm operator. The first of the index theorems gives an explicit formula for the Fredholm, or analytic, index
defines a continuous operator between suitable Sobolev spaces with closed range and finite-dimensional kernel and cokernel, that is, a Fredholm operator. The first of the index theorems gives an explicit formula for the Fredholm, or analytic, index  of
of 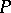 :
:
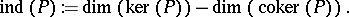 |
Denote by 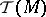 the Todd class of the complexification of the tangent bundle
the Todd class of the complexification of the tangent bundle 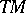 of
of 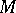 . If
. If 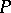 is an elliptic operator as above, its principal symbol
is an elliptic operator as above, its principal symbol 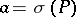 defines a
defines a 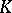 -theory class
-theory class 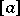 with compact supports on
with compact supports on 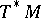 whose Chern character, denoted
whose Chern character, denoted 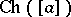 , is in the even cohomology of
, is in the even cohomology of 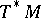 with compact supports. The Atiyah–Singer index formula of [a6] then states that
with compact supports. The Atiyah–Singer index formula of [a6] then states that
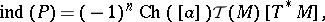 |
 being the dimension of the manifold
being the dimension of the manifold 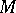 and
and 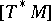 being the fundamental class of
being the fundamental class of 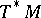 . (The factor
. (The factor 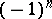 reflects the choice of the orientation of
reflects the choice of the orientation of 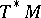 in the original articles. Other choices for this orientation will lead to different signs.) In other words, the index is obtained by evaluating the compactly supported cohomology class
in the original articles. Other choices for this orientation will lead to different signs.) In other words, the index is obtained by evaluating the compactly supported cohomology class 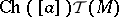 on the fundamental class of
on the fundamental class of 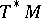 .
.
Equivariant index theorem.
The second of the index formulas refines the index when the operator 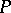 above is invariant with respect to a compact Lie group, see [a5], [a6]. Recall that the representation ring of a compact group
above is invariant with respect to a compact Lie group, see [a5], [a6]. Recall that the representation ring of a compact group 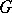 is defined as the ring of formal linear combinations with integer coefficients of equivalence classes of irreducible representations of
is defined as the ring of formal linear combinations with integer coefficients of equivalence classes of irreducible representations of 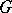 (cf. also Irreducible representation). For operators
(cf. also Irreducible representation). For operators 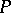 equivariant with respect to a compact group
equivariant with respect to a compact group 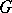 , the kernel and cokernel are representations of
, the kernel and cokernel are representations of 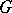 , so their difference can now be regarded as an element of
, so their difference can now be regarded as an element of 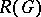 , called the equivariant index of
, called the equivariant index of 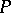 . The Atiyah–Singer index formula in [a6] gives the value
. The Atiyah–Singer index formula in [a6] gives the value 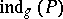 of the (character of the) index of
of the (character of the) index of 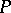 at
at 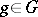 in terms of invariants of
in terms of invariants of 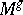 , the set of fixed points of
, the set of fixed points of 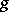 in
in 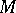 . Denote by
. Denote by 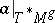 the restriction of
the restriction of  to the cotangent bundle of
to the cotangent bundle of 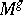 and by
and by 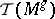 the Todd class of the complexification of the cotangent bundle of
the Todd class of the complexification of the cotangent bundle of 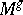 . In addition to these ingredients, which are similar to the ingredients appearing in the formula for
. In addition to these ingredients, which are similar to the ingredients appearing in the formula for 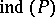 above, the formula for
above, the formula for 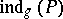 involves also a Lefschetz-type contribution, denoted below by
involves also a Lefschetz-type contribution, denoted below by 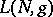 , obtained from the action of
, obtained from the action of 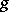 on the normal bundle to the set
on the normal bundle to the set 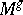 :
:
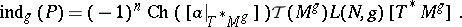 |
Families of elliptic operators.
For families of elliptic operators acting on the fibres of a fibre bundle 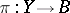 (cf. also Fibration), a first problem is to make sense of the index. The solution proposed by Atiyah and Singer in [a7] is to define the index as an element of a
(cf. also Fibration), a first problem is to make sense of the index. The solution proposed by Atiyah and Singer in [a7] is to define the index as an element of a 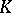 -theory group, namely
-theory group, namely 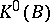 in this case (cf. also
in this case (cf. also 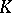 -theory). This fortunate choice has opened the way for many other developments in index theory. Actually, in the two index theorems mentioned above, the index can also be interpreted using a
-theory). This fortunate choice has opened the way for many other developments in index theory. Actually, in the two index theorems mentioned above, the index can also be interpreted using a 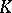 -theory group, the
-theory group, the 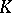 -theory of the algebra
-theory of the algebra 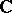 of complex numbers in the first index theorem and the
of complex numbers in the first index theorem and the 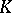 -theory group of
-theory group of 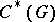 , the norm closure of the convolution algebra of
, the norm closure of the convolution algebra of 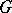 , in the equivariant index theorem. For the Chern character of the family index of a family of elliptic operators
, in the equivariant index theorem. For the Chern character of the family index of a family of elliptic operators 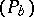 as above, there is a formula similar to the formula for the index of a single elliptic operator. The principal symbols
as above, there is a formula similar to the formula for the index of a single elliptic operator. The principal symbols 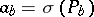 of the operators
of the operators 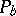 define, in this case, a class
define, in this case, a class 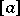 in the
in the 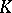 -theory with compact supports of
-theory with compact supports of 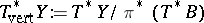 , the vertical cotangent bundle to the fibres of
, the vertical cotangent bundle to the fibres of 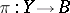 , as in the case of a single elliptic operator. Denote by
, as in the case of a single elliptic operator. Denote by 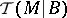 the Todd class of the complexification of
the Todd class of the complexification of 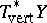 and by
and by 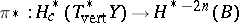 the morphism induced by integration along the fibres, with
the morphism induced by integration along the fibres, with  being the common dimension of the fibres of
being the common dimension of the fibres of 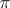 . Then
. Then
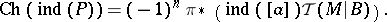 |
This completes the discussion of these three main theorems of Atiyah and Singer.
 -theory in index theory.
-theory in index theory.
The role of 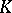 -theory in the proof and applications of the index theorems can hardly be overstated and certainly does not stop at providing an interpretation of the index as an element of a
-theory in the proof and applications of the index theorems can hardly be overstated and certainly does not stop at providing an interpretation of the index as an element of a 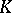 -theory group. A far-reaching consequence of the use of
-theory group. A far-reaching consequence of the use of 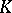 -theory, which depends on Bott periodicity (or more precisely, the Thom isomorphism, cf. also Bott periodicity theorem), is that all elliptic operators can be connected, by a homotopy of Fredholm operators, to certain operators of a very particular kind, the so-called generalized Dirac operators (see below). It is thus sufficient to prove the index theorems for generalized Dirac operators.
-theory, which depends on Bott periodicity (or more precisely, the Thom isomorphism, cf. also Bott periodicity theorem), is that all elliptic operators can be connected, by a homotopy of Fredholm operators, to certain operators of a very particular kind, the so-called generalized Dirac operators (see below). It is thus sufficient to prove the index theorems for generalized Dirac operators.
Due to their differential-geometric properties, it is possible to give more concrete proofs of the Atiyah–Singer index theorem for generalized Dirac operators, using heat kernels, for example (cf. also Heat content asymptotics). The generalized Dirac operator with coefficients in the spin bundle is called simply the Dirac operator (sometimes called the Atiyah–Singer operator). See below for more about generalized Dirac operators.
Applications of index theorems.
After the publication of the first papers by Atiyah and Singer, index theory has evolved into essentially three directions:
a direction which consists of applications and new proofs of the index theorems (especially "local" proofs using heat kernels);
a direction which studies invariants other than the index; and
a direction which aims at more general index theorems. There is a very large number of applications of index theorems to topology and other areas of mathematics. A few examples follow. In [a12], Atiyah and W. Schmid used Atiyah's 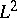 -index theorem for coverings [a11] to construct discrete series representations. In [a34], N.J. Hitchin used the families index theorem to prove that there exist metrics whose associated Dirac operators have non-trivial kernels (in suitable dimensions). An index theorem for foliations that is close in spirit to Atiyah's
-index theorem for coverings [a11] to construct discrete series representations. In [a34], N.J. Hitchin used the families index theorem to prove that there exist metrics whose associated Dirac operators have non-trivial kernels (in suitable dimensions). An index theorem for foliations that is close in spirit to Atiyah's 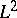 -index theorem was obtained by A. Connes [a27].
-index theorem was obtained by A. Connes [a27].
The index of Dirac (or Atiyah–Singer) operators was used to formulate and then prove the Gromov–Lawson conjecture [a32], which states that a compact, spin, simply connected manifold of dimension 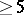 admits a metric of positive scalar curvature if and only if the index of the spin Dirac operator (in an appropriate
admits a metric of positive scalar curvature if and only if the index of the spin Dirac operator (in an appropriate 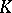 -theory group) is zero. This conjecture was proved by S. Stolz, [a48]. Dirac operators have been used to give a concrete construction of
-theory group) is zero. This conjecture was proved by S. Stolz, [a48]. Dirac operators have been used to give a concrete construction of 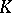 -homology [a16].
-homology [a16].
Some of the applications of the index theorems require new proofs of these theorems, usually relying on the "heat-kernel method" . The main idea of this method is as follows. H. McKean and Singer [a39] stated the problem of investigating the behaviour, as 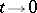 ,
, 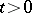 , of the (super-trace of the) heat kernel. More precisely, let
, of the (super-trace of the) heat kernel. More precisely, let
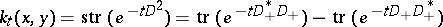 |
be the well-known term appearing in the McKean–Singer index formula, where  is a self-adjoint geometric operator (cf. also Self-adjoint operator) with
is a self-adjoint geometric operator (cf. also Self-adjoint operator) with 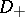 mapping the subspace of even sections to the subspace of odd sections. They considered the case of the de Rham operator
mapping the subspace of even sections to the subspace of odd sections. They considered the case of the de Rham operator 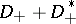 , where
, where 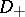 is then the de Rham differential (cf. also de Rham cohomology). It was known that the integral over the whole manifold of
is then the de Rham differential (cf. also de Rham cohomology). It was known that the integral over the whole manifold of 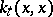 gives the analytic index of
gives the analytic index of 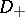 , and they expressed the hope that
, and they expressed the hope that 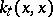 will have a definite limit as
will have a definite limit as 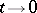 . This was proved for various particular cases by V. Patodi in [a54] and then by P. Gilkey [a29], [a30] using invariant theory (see [a31] for an exposition of this method). This method was finally refined in [a1] to give a clear and elegant proof of the local index theorem for all Dirac operators.
. This was proved for various particular cases by V. Patodi in [a54] and then by P. Gilkey [a29], [a30] using invariant theory (see [a31] for an exposition of this method). This method was finally refined in [a1] to give a clear and elegant proof of the local index theorem for all Dirac operators.
Inspired by a talk of Atiyah, J.-M. Bismut investigated connections between probability theory and index theory. He was able to use the stochastic calculus (cf. also Malliavin calculus) to give a new proof of the local index theorem [a17]. His methods then generalized to give proofs of the local index theorem for families of Dirac operators [a18] using Quillen's theory of super-connections [a43], and of the Atiyah–Bott fixed-point formulas [a19]. An application of his results is the determination of the Quillen metric on the determinant bundle [a21].
The local index theorems have many connections to physics, where Dirac operators play a prominent role. Actually, several physicists have come up with arguments for a proof of the local index theorem based on supersymmetry and functional integration, see [a8] and [a53], for example. Building on these arguments, E. Getzler has obtained a short and elegant proof of the local index theorem [a14], [a31], which also uses supersymmetry. Moreover, ideas inspired from physics have lead E. Witten to conjecture that certain twisted Dirac operators on 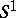 -manifolds have an index that is a trivial representation of
-manifolds have an index that is a trivial representation of 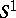 , see [a52]. This was proved by C.H. Taubes [a49] (see also [a23] and [a51]). For the Dirac operator, this had been proved before by Atiyah and F. Hirzebruch [a2].
, see [a52]. This was proved by C.H. Taubes [a49] (see also [a23] and [a51]). For the Dirac operator, this had been proved before by Atiyah and F. Hirzebruch [a2].
Other invariants.
Heat-kernel methods have proved very useful in dealing with non-compact and singular spaces. A common feature of these spaces is that the index formulas for the natural operators on them depend on more than just the principal symbol, which leads to the appearance of non-local invariants in these index formulas. In general, there exists no good understanding, at this time (2000), of what these non-local invariants are, except in particular cases. The most prominent of these particular cases is the Atiyah–Patodi–Singer index theorem for manifolds with boundary. Other results in these directions were obtained in [a25], [a40], [a41], [a47]. In all these cases, eta-invariants of certain boundary operators must be included in the formula for the index. Moreover, one has to either work on complete manifolds or to include boundary conditions to make the given problems Fredholm. The Atiyah–Patodi–Singer index theorem [a3], e.g., requires such boundary conditions; see below.
Let 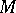 be a compact manifold with boundary
be a compact manifold with boundary  and metric
and metric 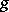 which is a product metric in a suitable cylindrical neighbourhood of
which is a product metric in a suitable cylindrical neighbourhood of 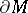 . Fix a Clifford module
. Fix a Clifford module 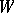 on
on 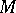 (cf. also Clifford algebra) and an admissible connection
(cf. also Clifford algebra) and an admissible connection  . Denote by
. Denote by 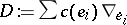 the generalized Dirac operator on
the generalized Dirac operator on 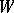 , where
, where 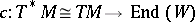 is the Clifford multiplication and
is the Clifford multiplication and  is a local orthonormal basis (cf. also Orthogonal basis). Also, let
is a local orthonormal basis (cf. also Orthogonal basis). Also, let  be the corresponding generalized Dirac operator on
be the corresponding generalized Dirac operator on 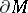 , which is (essentially) self-adjoint because
, which is (essentially) self-adjoint because 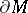 is compact without boundary. Then the eigenvalues of
is compact without boundary. Then the eigenvalues of 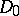 will form a discrete subset of the real numbers; denote by
will form a discrete subset of the real numbers; denote by 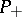 the spectral projection corresponding to the eigenvalues of
the spectral projection corresponding to the eigenvalues of 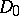 that are
that are 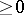 . Decompose
. Decompose 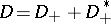 using the natural
using the natural 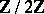 -grading on
-grading on 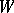 . The operator
. The operator 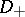 , the chiral Dirac operator, acts from sections of
, the chiral Dirac operator, acts from sections of 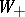 to sections of
to sections of 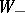 , and has an infinite-dimensional kernel. Because of that, Atiyah, Patodi and Singer have introduced a non-local boundary condition of the form
, and has an infinite-dimensional kernel. Because of that, Atiyah, Patodi and Singer have introduced a non-local boundary condition of the form 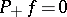 , for
, for 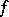 a smooth section of
a smooth section of 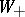 over
over 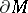 , which is a compact perturbation of the Calderón projection boundary condition. The effect of this boundary condition is that the restriction of
, which is a compact perturbation of the Calderón projection boundary condition. The effect of this boundary condition is that the restriction of 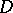 to the subspace of sections satisfying this boundary condition is Fredholm. Assume that
to the subspace of sections satisfying this boundary condition is Fredholm. Assume that 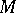 is
is 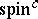 with spinor bundle
with spinor bundle 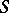 , such that
, such that 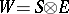 , and let
, and let 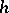 denote the dimension of the kernel of
denote the dimension of the kernel of 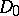 . The index of the resulting operator
. The index of the resulting operator 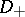 with the above boundary conditions is then
with the above boundary conditions is then
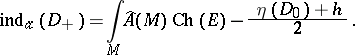 |
This formula was generalized by Bismut and J. Cheeger in [a20] to families of manifolds with boundary, the result being expressed using the "eta form" 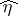 . More precisely, using the notation above, they proved that
. More precisely, using the notation above, they proved that
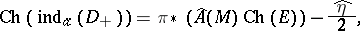 |
provided that all Dirac operator associated to the boundaries of the fibres are invertible.
Presently (2000), cyclic homology (cf. also Cyclic cohomology) is probably the only general tool to deal with index problems in which the index belongs to an abstract, possibly unknown, 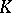 -theory group, or to deal with index theorems involving non-local invariants. See [a26], [a36], [a38], or [a50] for the basic results on cyclic homology. The relation between the
-theory group, or to deal with index theorems involving non-local invariants. See [a26], [a36], [a38], or [a50] for the basic results on cyclic homology. The relation between the  -theory of the algebra
-theory of the algebra 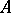 and the cyclic homology of
and the cyclic homology of 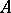 is via Chern characters
is via Chern characters  ,
,  , and is due to Connes and M. Karoubi.
, and is due to Connes and M. Karoubi.
Generalized index theorems.
In [a24], Connes and H. Moscovici have generalized Atiyah's 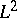 -index theorem, which allowed them to obtain a proof of the Novikov conjecture (cf. also
-index theorem, which allowed them to obtain a proof of the Novikov conjecture (cf. also 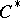 -algebra) for certain classes of groups. The index theorem, also called the higher index theorem for coverings, is as follows. Let
-algebra) for certain classes of groups. The index theorem, also called the higher index theorem for coverings, is as follows. Let 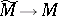 be a covering of a compact manifold
be a covering of a compact manifold 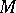 with group of deck transformations
with group of deck transformations 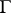 (cf. also Monodromy transformation). If
(cf. also Monodromy transformation). If 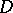 is an elliptic differential operator on
is an elliptic differential operator on 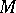 invariant with respect to
invariant with respect to 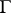 (such as the signature operator), then it has an index
(such as the signature operator), then it has an index 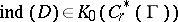 , the
, the 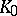 -group of the closure of the group algebra of
-group of the closure of the group algebra of 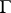 acting on
acting on 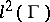 . This index was defined by A.T. Fomenko and A. Mishchenko in [a28]. This index can be refined to an index in
. This index was defined by A.T. Fomenko and A. Mishchenko in [a28]. This index can be refined to an index in 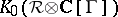 , where
, where 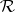 is the algebra of infinite matrices with complex entries and with rapid decrease. Using cyclic cohomology and the Chern character in cyclic homology, every cohomology class
is the algebra of infinite matrices with complex entries and with rapid decrease. Using cyclic cohomology and the Chern character in cyclic homology, every cohomology class 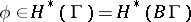 gives rise to a morphism
gives rise to a morphism 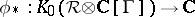 , and the problem is to determine
, and the problem is to determine 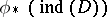 . If
. If 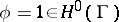 , then this number is exactly the von Neumann index appearing in Atiyah's
, then this number is exactly the von Neumann index appearing in Atiyah's 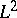 -index formula.
-index formula.
Let 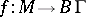 be the mapping that classifies the covering
be the mapping that classifies the covering 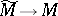 and let
and let 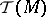 be the Todd class of the complexification of
be the Todd class of the complexification of 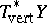 . If
. If 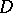 is an elliptic invariant differential operator, its principal symbol
is an elliptic invariant differential operator, its principal symbol 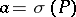 defines a
defines a 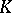 -theory class
-theory class 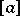 with compact supports on
with compact supports on 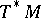 , whose Chern character
, whose Chern character  is in the even cohomology of
is in the even cohomology of 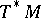 with compact supports, as in the case of the Atiyah–Singer index theorem for a single elliptic operator. Suppose
with compact supports, as in the case of the Atiyah–Singer index theorem for a single elliptic operator. Suppose 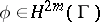 ; then the Connes–Moscovici higher index theorem for coverings [a24] states that
; then the Connes–Moscovici higher index theorem for coverings [a24] states that
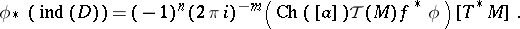 |
The Chern character in cyclic cohomology turns out to be a natural mapping, and this can be interpreted as a general index theorem in cyclic cohomology [a42]. It is hoped that this general index theorem will help explain the ubiquity of the Todd class in index theorems.
For more information on index theory, see, e.g., [a14], [a15], [a45]. To get a balanced point of view, see also [a13] for an account of the original approach to the Atiyah–Singer index theorems, which also gives all the necessary background a student needs.
References
| [a1] | M. Atiyah, R. Bott, V. Patodi, "On the heat equation and the index theorem" Invent. Math. , 19 (1973) pp. 279–330 (Erata ibid. 28 (1975), 277-280) |
| [a2] | M. Atiyah, F. Hirzebruch, "Spin manifolds and group actions" , Essays in Topology and Related subjects , Springer (1994) pp. 18–28 |
| [a3] | M. Atiyah, V. Patodi, I. Singer, "Spectral asymmetry and Riemannian geometry I" Math. Proc. Cambridge Philos. Soc. , 77 (1975) pp. 43–69 |
| [a4] | M. Atiyah, I. Singer, "The index of elliptic operators I" Ann. of Math. , 87 (1968) pp. 484–530 |
| [a5] | M. Atiyah, G. Segal, "The index of elliptic operators II" Ann. of Math. , 87 (1968) pp. 531–545 |
| [a6] | M. Atiyah, I. Singer, "The index of elliptic operators III" Ann. of Math. , 93 (1968) pp. 546–604 |
| [a7] | M. Atiyah, I. Singer, "The index of elliptic operators IV" Ann. of Math. , 93 (1971) pp. 119–138 |
| [a8] | L. Alvarez-Gaumé, "Supersymmetry and the Atiyah–Singer index theorem" Comm. Math. Phys. , 90 (1983) pp. 161–173 |
| [a9] | M. Atiyah, R. Bott, "A Lefschetz fixed-point formula for elliptic complexes II: Applications." Ann. of Math. , 88 (1968) pp. 451–491 |
| [a10] | M. Atiyah, "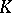 -theory" , Benjamin (1967) -theory" , Benjamin (1967) |
| [a11] | M. Atiyah, "Elliptic operators, discrete subgroups, and von Neumann algebras" Astérisque , 32/33 (1969) pp. 43–72 |
| [a12] | M. Atiyah, W. Schmid, "A geometric construction of the discrete series" Invent. Math. , 42 (1977) pp. 1–62 |
| [a13] | B. Booss–Bavnbek, D. Bleecker, "Topology and analysis. The Atiyah–Singer index formula and gauge-theoretic physics" , Universitext , Springer (1985) |
| [a14] | N. Berline, E. Getzler, M. Vèrgne, "Heat kernels and Dirac operator" , Grundl. Math. Wissenschaft. , 298 , Springer (1996) |
| [a15] | B. Booss–Bavnbek, K. Wojciechowski, "Elliptic boundary problems for Dirac operators" , Math. Th. Appl. , Birkhäuser (1993) |
| [a16] | P. Baum, R. Douglas, "Index theory, bordism, and 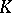 -homology" , Operator Algebras and -homology" , Operator Algebras and 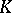 -Theory (San Francisco, Calif., 1981) , Contemp. Math. , 10 , Amer. Math. Soc. (1982) pp. 1–31 -Theory (San Francisco, Calif., 1981) , Contemp. Math. , 10 , Amer. Math. Soc. (1982) pp. 1–31 |
| [a17] | J.-M. Bismut, "The Atiyah–Singer theorems: a probabilistic approach" J. Funct. Anal. , 57 (1984) pp. 56–99 |
| [a18] | J.-M. Bismut, "The index theorem for families of Dirac operators: two heat equation proofs" Invent. Math. , 83 (1986) pp. 91–151 |
| [a19] | J.-M. Bismut, "The Atiyah–Singer theorems: a probabilistic approach. II. The Lefschetz fixed point formulas" J. Funct. Anal. , 57 : 3 (1984) pp. 329–348 |
| [a20] | J.-M. Bismut, J. Cheeger, "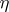 -invariants and their adiabatic limits" J. Amer. Math. Soc. , 2 (1989) pp. 33–70 -invariants and their adiabatic limits" J. Amer. Math. Soc. , 2 (1989) pp. 33–70 |
| [a21] | J.-M. Bismut, D. Freed, "The analysis of elliptic families: Metrics and connections on determinant bundles" Comm. Math. Phys. , 106 (1986) pp. 103–163 |
| [a22] | A. Borel, J.-P. Serre, "Le téorème de Riemann–Roch (d'apreès Grothendieck)" Bull. Soc. Math. France , 86 (1958) pp. 97–136 |
| [a23] | R. Bott, C. Taubes, "On the rigidity theorems of Witten" J. Amer. Math. Soc. , 2 : 1 (1989) pp. 137–186 |
| [a24] | A. Connes, H. Moscovici, "Cyclic cohomology, the Novikov conjecture and hyperbolic groups" Topology , 29 (1990) pp. 345–388 |
| [a25] | J. Cheeger, "On the Hodge theory of Riemannian pseudomanifolds" , Geometry of the Laplace operator (Univ. Hawaii, 1979) , Proc. Symp. Pure Math. , XXXVI , Amer. Math. Soc. (1980) pp. 91–146 |
| [a26] | A. Connes, "Non-commutative differential geometry" Publ. Math. IHES , 62 (1985) pp. 41–144 |
| [a27] | A. Connes, "Sur la théorie noncommutative de l'intégration" , Algèbres d'Opérateurs , Lecture Notes in Mathematics , 725 , Springer (1982) pp. 19–143 |
| [a28] | A. Miščenko, A. Fomenko, "The index of elliptic operators over 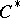 -algebras" Izv. Akad. Nauk. SSSR Ser. Mat. , 43 (1979) pp. 831–859 -algebras" Izv. Akad. Nauk. SSSR Ser. Mat. , 43 (1979) pp. 831–859 |
| [a29] | P. Gilkey, "Curvature and the eigenvalues of the Laplacian for elliptic complexes" Adv. Math. , 10 (1973) pp. 344–382 |
| [a30] | P. Gilkey, "Curvature and the eigenvalues of the Dolbeault complex for Kaehler manifolds" Adv. Math. , 11 (1973) pp. 311–325 |
| [a31] | P. Gilkey, "Invariance theory, the heat equation, and the Atiyah–Singer index theorem" , CRC (1994) |
| [a32] | M. Gromov, H. Lawson Jr., "The classification of simply connected manifolds of positive scalar curvature" Ann. of Math. , 111 (1980) pp. 423–434 |
| [a33] | F. Hirzebruch, "Topological methods in algebraic geometry" , Grundl. Math. Wissenschaft. , 131 , Springer (1966) (Edition: Third) |
| [a34] | N. Hitchin, "Harmonic spinors" Adv. Math. , 14 (1974) pp. 1–55 |
| [a35] | L. Hörmander, "Pseudo-differential operators" Commun. Pure Appl. Math. , 18 (1965) pp. 501–517 |
| [a36] | M. Karoubi, "Homology cyclique et K-theorie" Astérisque , 149 (1987) pp. 1–147 |
| [a37] | J. Kohn, L. Nirenberg, "An algebra of pseudodifferential operators" Commun. Pure Appl. Math. , 18 (1965) pp. 269–305 |
| [a38] | J.-L. Loday, D. Quillen, "Cyclic homology and the Lie homology of matrices" Comment. Math. Helv. , 59 (1984) pp. 565–591 |
| [a39] | H. McKean Jr., I. Singer, "Curvature and the eigenvalues of the Laplacian" J. Diff. Geom. , 1 (1967) pp. 43–69 |
| [a40] | R. Melrose, "The Atiyah–Patodi–Singer index theorem" , Peters (1993) |
| [a41] | W. Müller, "Manifolds with cusps of rank one, spectral theory and an 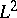 -index theorem" , Lecture Notes in Mathematics , 1244 , Springer (1987) -index theorem" , Lecture Notes in Mathematics , 1244 , Springer (1987) |
| [a42] | V. Nistor, "Higher index theorems and the boundary map in cyclic cohomology" Documenta Math. (1997) pp. 263–296 ((electronic)) |
| [a43] | D. Quillen, "Superconnections and the Chern character" Topology , 24 (1985) pp. 89–95 |
| [a44] | D. Ray, I. Singer, "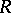 -torsion and the laplacian on Riemannian manifolds" Adv. Math. , 7 (1971) pp. 145–210 -torsion and the laplacian on Riemannian manifolds" Adv. Math. , 7 (1971) pp. 145–210 |
| [a45] | J. Roe, "Elliptic operators, topology and asymptotic methods" , Pitman Res. Notes in Math. Ser. , 179 , Longman (1988) |
| [a46] | R.T. Seeley, "Refinement of the functional calculus of Calderòn and Zygmund" Indag. Math. , 27 (1965) pp. 521–531 Nederl. Akad. Wetensch. Proc. Ser. A , 68 (1965) |
| [a47] | Mark Stern, "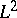 -index theorems on locally symmetric spaces" Invent. Math. , 96 (1989) pp. 231–282 -index theorems on locally symmetric spaces" Invent. Math. , 96 (1989) pp. 231–282 |
| [a48] | S. Stolz, "Simply connected manifolds of positive scalar curvature" Ann. of Math. , 136 : 2 (1992) pp. 511–540 |
| [a49] | C. Taubes, "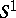 actions and elliptic genera" Comm. Math. Phys. , 122 (1989) pp. 455–526 actions and elliptic genera" Comm. Math. Phys. , 122 (1989) pp. 455–526 |
| [a50] | B.L. Tsygan, "Homology of matrix Lie algebras over rings and Hochschild homology" Uspekhi Mat. Nauk. , 38 (1983) pp. 217–218 |
| [a51] | E. Witten, "Supersymmetry and Morse theory" J. Diff. Geom. , 17 (1982) pp. 661–692 |
| [a52] | E. Witten, "Elliptic genera and quantum field theory" Comm. Math. Phys. , 109 (1987) pp. 525–536 |
| [a53] | E. Witten, "Constraints on supersymmetry breaking" Nucl. Phys. B , 202 (1982) pp. 253–316 |
| [a54] | V. Patodi, "Curvature and the eigenforms of the Laplace operator" J. Diff. Geom. , 5 (1971) pp. 233–249 |
Index theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Index_theory&oldid=12180