Indefinite limits and expressions, evaluations of
Methods for computing limits of functions given by formulas that cease to have a meaning when the limiting values of the argument are formally substituted in them, that is, go over into expressions like
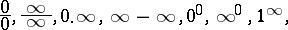 |
for which one cannot judge whether the required limits exist or not without saying anything about finding their values if they exist. The basic instrument of evaluating indeterminacies is Taylor's formula (cf. Taylor formula), by means of which one singles out the principal part of a function. Thus, in the case of an indeterminacy of the type  , for which in order to find the limit
, for which in order to find the limit
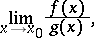 |
where
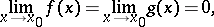 |
one represents the functions  and
and  by Taylor's formulas in a neighbourhood of
by Taylor's formulas in a neighbourhood of  (if this is possible) up to the first non-zero term:
(if this is possible) up to the first non-zero term:
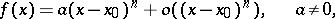 |
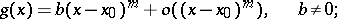 |
as a result one finds that
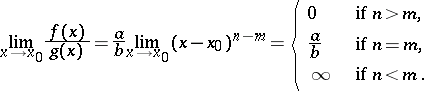 |
In the case of an indeterminacy of the type 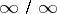 , in order to find the limit
, in order to find the limit
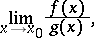 |
where
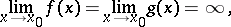 |
one applies the transformation
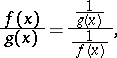 |
which reduces the problem to the evaluation of an indeterminacy of type  .
.
Indeterminacies of the types 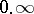 or
or 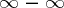 are also conveniently reduced to type
are also conveniently reduced to type 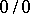 by the following transformations:
by the following transformations:
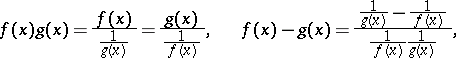 |
respectively.
For evaluating indeterminacies of the types 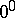 ,
, 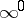 or
or 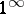 it is appropriate first to take the logarithm of the expressions whose limits are to be found.
it is appropriate first to take the logarithm of the expressions whose limits are to be found.
Another general method for evaluating indeterminacies of the types 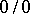 or
or 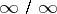 and those reducible to them is the l'Hospital rule.
and those reducible to them is the l'Hospital rule.
Comments
References
| [a1] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
Indefinite limits and expressions, evaluations of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Indefinite_limits_and_expressions,_evaluations_of&oldid=15291