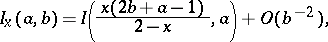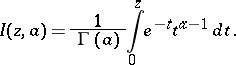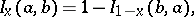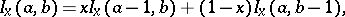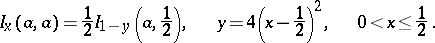The function defined by the formula
where
is the beta-function. If  is an integer, then
is an integer, then
Series representation:
Continued fraction representation:
where
Asymptotic representation for large  and
and 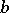 :
:
where
Asymptotic representation for large 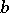 and bounded
and bounded  :
:
where
Connection with the hypergeometric function:
Recurrence relations:
References
| [1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1973) |
| [2] | K. Pearson, "Tables of the incomplete beta-function" , Cambridge Univ. Press (1932) |
How to Cite This Entry:
Incomplete beta-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Incomplete_beta-function&oldid=16063
This article was adapted from an original article by V.I. Pagurova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article
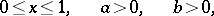
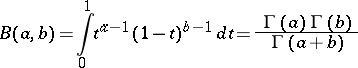
 is an integer, then
is an integer, then
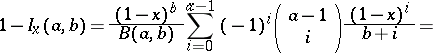

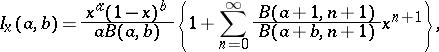

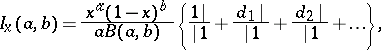
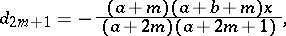
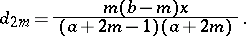
 and
and 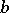 :
:
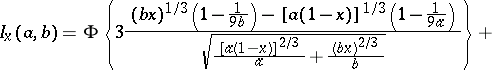
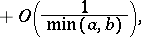
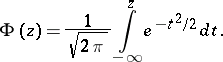
 and bounded
and bounded  :
: