Immersion of a manifold
A continuous mapping 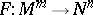 of an
of an  -dimensional manifold
-dimensional manifold  into an
into an  -dimensional manifold
-dimensional manifold  such that for each point
such that for each point  there exists a neighbourhood
there exists a neighbourhood  in which
in which  is an imbedding, i.e. a homeomorphism onto
is an imbedding, i.e. a homeomorphism onto  . In particular, if
. In particular, if 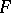 is a homeomorphism into
is a homeomorphism into 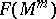 , then it is called an imbedding of
, then it is called an imbedding of 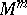 in
in  . The immersion
. The immersion 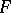 is called a
is called a 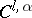 -immersion if
-immersion if  and
and 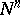 are
are  -(smooth) manifolds (
-(smooth) manifolds (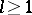 ,
, 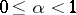 ,
, 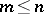 ) and if the mapping
) and if the mapping  on the corresponding charts is given by functions
on the corresponding charts is given by functions
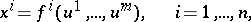 |
that belong to the smoothness class 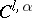 , while the rank of the matrix
, while the rank of the matrix  is equal to
is equal to 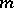 at each point
at each point 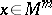 (a
(a  -(smooth) manifold is a manifold provided with a
-(smooth) manifold is a manifold provided with a 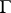 -structure, where the pseudo-group consists of mappings that are
-structure, where the pseudo-group consists of mappings that are 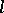 -times differentiable and whose derivatives satisfy the Hölder condition of index
-times differentiable and whose derivatives satisfy the Hölder condition of index 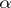 ).
).
The concepts of a surface and a 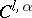 -(smooth) surface are closely related to the concepts of an immersion and a
-(smooth) surface are closely related to the concepts of an immersion and a 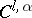 -(smooth) immersion. Two immersions
-(smooth) immersion. Two immersions  and
and  between manifolds
between manifolds 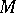 and
and 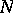 are called equivalent if there is a homeomorphism
are called equivalent if there is a homeomorphism 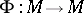 such that
such that 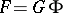 .
.
An immersed manifold is a pair consisting of a manifold  and an immersion
and an immersion 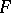 of it. A surface of dimension
of it. A surface of dimension 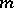 in a manifold
in a manifold 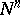 of dimension
of dimension  is a class of equivalent immersions
is a class of equivalent immersions  ; each immersion of this class is called a parametrization of the surface. A surface is called
; each immersion of this class is called a parametrization of the surface. A surface is called 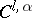 -smooth if one can introduce
-smooth if one can introduce 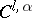 -structures in the manifolds
-structures in the manifolds 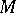 and
and 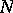 and if among the parametrizations of the surface one can find a parametrization
and if among the parametrizations of the surface one can find a parametrization  which in these structures is a
which in these structures is a  -immersion.
-immersion.
The theory of immersed manifolds usually deals with properties that are invariant under the above concept of equivalence, and in essence coincides with the theory of surfaces, particularly when one considers topics related to the geometry of immersions.
Let 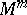 be a
be a  -manifold,
-manifold, 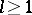 ,
, 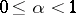 . Any
. Any  allows for
allows for 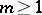 an imbedding into the Euclidean space
an imbedding into the Euclidean space 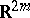 and a
and a 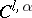 -immersion into
-immersion into  for
for  . If
. If 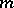 is positive and not a power of
is positive and not a power of  , then any
, then any 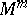 allows a
allows a 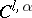 -imbedding into
-imbedding into 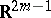 , whereas for any
, whereas for any 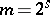 with
with 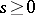 there exist closed smooth
there exist closed smooth 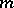 -dimensional manifolds not allowing even a topological imbedding into
-dimensional manifolds not allowing even a topological imbedding into 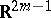 (such as, for example, a projective space). If
(such as, for example, a projective space). If 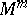 does not have compact components, it allows a
does not have compact components, it allows a  -imbedding into
-imbedding into 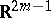 .
.
An orientable 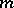 -dimensional manifold for
-dimensional manifold for  allows a
allows a 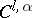 -imbedding into
-imbedding into 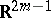 . The possibility of immersing an
. The possibility of immersing an 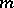 -dimensional manifold into
-dimensional manifold into 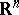 for
for 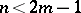 is related to the Whitney and Pontryagin classes (cf. Pontryagin class) of this manifold. Also, each
is related to the Whitney and Pontryagin classes (cf. Pontryagin class) of this manifold. Also, each 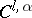 -smooth
-smooth  -dimensional manifold with
-dimensional manifold with  ,
, 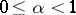 allows a proper immersion into
allows a proper immersion into  and a proper imbedding into
and a proper imbedding into 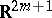 (i.e. an immersion or imbedding such that the pre-image of each compact set is compact). If a Riemannian metric is given on
(i.e. an immersion or imbedding such that the pre-image of each compact set is compact). If a Riemannian metric is given on 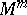 , one frequently considers an isometric immersion of
, one frequently considers an isometric immersion of 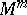 into
into 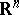 or into another Riemannian space
or into another Riemannian space  . A
. A 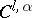 -smooth Riemannian manifold (
-smooth Riemannian manifold (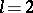 ,
, 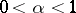 ;
; 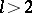 ,
, 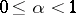 ) allows a
) allows a 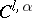 -smooth isometric immersion into some
-smooth isometric immersion into some 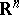 . In the case of a compact
. In the case of a compact 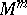 ,
, 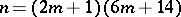 . Conversely, a
. Conversely, a 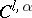 -smooth immersion of
-smooth immersion of 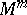 into
into 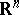 (
(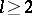 ,
, 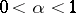 ) induces a
) induces a  -smooth Riemannian metric on
-smooth Riemannian metric on 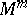 [4].
[4].
References
| [1] | S. Smale, "The classification of spheres in Euclidean spaces" Ann. of Math. , 69 (1959) pp. 327–344 |
| [2] | H. Jacobowitz, "Implicit function theorems and isometric embeddings" Ann. of Math. , 95 (1972) pp. 191–225 |
| [3] | V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian) |
| [4] | I.Kh. Sabitov, S.Z. Shefel', "The connections between the order of smoothness of a surface and its metric" Sib. Math. J. , 17 : 4 (1976) pp. 687–694 Sibirsk. Mat. Zh. , 17 : 4 (1976) pp. 916–925 |
Comments
References
| [a1] | J. Nash, "The embedding problem for Riemannian manifolds" Ann. of Math. , 63 (1956) pp. 20–63 |
Immersion of a manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Immersion_of_a_manifold&oldid=47318