Immersion
A mapping  of one topological space into another for which each point of
of one topological space into another for which each point of  has a neighbourhood
has a neighbourhood  which is homeomorphically mapped onto
which is homeomorphically mapped onto  by
by  . This concept is applied mainly to mappings of manifolds, where one often additionally requires a local flatness condition (as for a locally flat imbedding). The latter condition is automatically fulfilled if the manifolds
. This concept is applied mainly to mappings of manifolds, where one often additionally requires a local flatness condition (as for a locally flat imbedding). The latter condition is automatically fulfilled if the manifolds  and
and  are differentiable and if the Jacobi matrix of the mapping
are differentiable and if the Jacobi matrix of the mapping  has maximum rank, equal to the dimension of
has maximum rank, equal to the dimension of  at each point. The classification of immersions of one manifold into another up to a regular homotopy can be reduced to a pure homotopic problem. A homotopy
at each point. The classification of immersions of one manifold into another up to a regular homotopy can be reduced to a pure homotopic problem. A homotopy 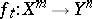 is called regular if for each point
is called regular if for each point  it can be continued to an isotopy (in topology)
it can be continued to an isotopy (in topology) 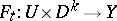 , where
, where 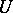 is a neighbourhood of
is a neighbourhood of  ,
, 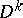 is a disc of dimension
is a disc of dimension 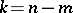 and
and 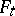 coincides with
coincides with 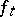 on
on  , where 0 is the centre of the disc. In the differentiable case, it is sufficient to require that the Jacobi matrix has maximum rank for each
, where 0 is the centre of the disc. In the differentiable case, it is sufficient to require that the Jacobi matrix has maximum rank for each  and depends continuously on
and depends continuously on  . The differential
. The differential 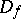 of an immersion determines a fibre-wise monomorphism of the tangent bundle
of an immersion determines a fibre-wise monomorphism of the tangent bundle 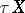 into the tangent bundle
into the tangent bundle 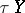 . A regular homotopy determines a homotopy of such monomorphisms. This establishes a bijection between the classes of regular homotopies and the homotopy classes of monomorphisms of bundles.
. A regular homotopy determines a homotopy of such monomorphisms. This establishes a bijection between the classes of regular homotopies and the homotopy classes of monomorphisms of bundles.
The problem of immersions in a Euclidean space reduces to the homotopy classification of mappings into a Stiefel manifold  . For example, because
. For example, because 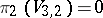 , there is only one immersion class of the sphere
, there is only one immersion class of the sphere 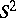 into
into 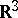 , so the standard imbedding is regularly homotopic to its mirror reflection (the sphere may be regularly turned inside out. Because
, so the standard imbedding is regularly homotopic to its mirror reflection (the sphere may be regularly turned inside out. Because  , there is a countable number of immersion classes of a circle into the plane, and because the Stiefel fibration over
, there is a countable number of immersion classes of a circle into the plane, and because the Stiefel fibration over 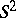 is homeomorphic to the projective space
is homeomorphic to the projective space 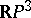 and
and 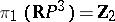 , there are only two immersion classes from
, there are only two immersion classes from 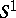 into
into 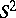 , etc.
, etc.
Comments
For figures illustrating the fact that 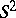 can be regularly turned inside out see [a3].
can be regularly turned inside out see [a3].
References
| [a1] | M.L. Gromov, "Stable mappings of foliations into manifolds" Math. USSR Izv. , 3 (1969) pp. 671–694 Izv. Akad. Nauk SSSR , 33 (1969) pp. 707–734 |
| [a2] | V. Poénaru, "Homotopy theory and differentiable singularities" N.H. Kuiper (ed.) , Manifolds (Amsterdam, 1970) , Lect. notes in math. , 197 , Springer (1971) pp. 106–132 |
| [a3] | A. Phillips, "Turning a surface inside out" Scientific Amer. , May (1966) pp. 112–120 |
Immersion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Immersion&oldid=17052