Imbedding theorems for Orlicz-Sobolev spaces
Establishing imbedding theorems goes back to T.K. Donaldson and N.S. Trudinger, and R.A. Adams (see [a4], [a10], [a2]). For the sake of simplicity, consider the space  with an
with an  -function
-function  (cf. Orlicz–Sobolev space), where
(cf. Orlicz–Sobolev space), where  is sufficiently smooth (a Lipschitz boundary, for instance; see [a1]). Define
is sufficiently smooth (a Lipschitz boundary, for instance; see [a1]). Define  ,
,  . The case
. The case  corresponds to the sublimiting case for usual Sobolev spaces (cf. also Sobolev space) and in this case
corresponds to the sublimiting case for usual Sobolev spaces (cf. also Sobolev space) and in this case  is imbedded into
is imbedded into  , where
, where 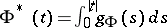 ,
,  . The case
. The case 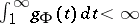 corresponds to
corresponds to  for
for 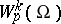 . If one defines the generalized Hölder spaces
. If one defines the generalized Hölder spaces 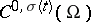 , where
, where 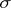 is a increasing continuous function on
is a increasing continuous function on 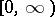 such that
such that 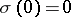 , as the space of continuous functions on
, as the space of continuous functions on  , for which
, for which 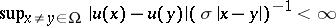 , then the target space for the imbeddings is a Hölder space of this type with
, then the target space for the imbeddings is a Hölder space of this type with  .
.
A (partial) ordering of such functions  (and of
(and of 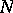 -functions) can be introduced in the following way: If
-functions) can be introduced in the following way: If  and
and 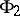 are
are 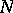 -functions, then
-functions, then 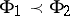 if
if 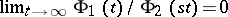 for every
for every  . Further,
. Further, 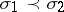 if
if 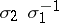 is a function of the same type. If now
is a function of the same type. If now  is imbedded into
is imbedded into 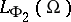 and
and 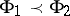 , then
, then 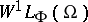 is compactly imbedded into
is compactly imbedded into  , and if
, and if 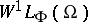 is imbedded into
is imbedded into 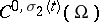 and
and 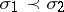 , then
, then 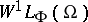 is compactly imbedded into
is compactly imbedded into  .
.
The sublimiting case was handled also by the method of Fourier analysis (cf. e.g. [a9], [a8]), by considering potential Orlicz–Sobolev spaces (nevertheless, in this case non-reflexive spaces are excluded). The problem of the best target space in the scale of Orlicz spaces has been dealt with in, e.g., [a3]). Recently (1998), logarithmic Sobolev spaces, which are nothing but Orlicz–Sobolev spaces with generating function of the type 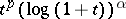 , tuning the scale of Sobolev spaces, have been used in connection with limiting imbeddings into exponential Orlicz spaces and/or logarithmic Lipschitz spaces (see, e.g., [a7], [a5], [a6]).
, tuning the scale of Sobolev spaces, have been used in connection with limiting imbeddings into exponential Orlicz spaces and/or logarithmic Lipschitz spaces (see, e.g., [a7], [a5], [a6]).
There are, however, still many open problems in the theory. Apart from difficulties of rather technical nature, the whole scale of these spaces presumably cannot be handled by known methods of interpolation and/or extrapolation of Sobolev spaces or even more general Besov or Triebel–Lizorkin spaces.
References
| [a1] | R.A. Adams, "Sobolev spaces" , Acad. Press (1975) |
| [a2] | R.A. Adams, "General logarithmic Sobolev inequalities and Orlicz imbeddings" J. Funct. Anal. , 34 (1979) pp. 292–303 |
| [a3] | A. Cianchi, "A sharp embedding theorem for Orlicz–Sobolev spaces" Indiana Univ. Math. J. , 45 (1996) pp. 39–65 |
| [a4] | T.K. Donaldson, N.S. Trudinger, "Orlicz–Sobolev spaces and imbedding theorems" J. Funct. Anal. , 8 (1971) pp. 52–75 |
| [a5] | D.E. Edmunds, M. Krbec, "Two limiting cases of Sobolev imbeddings" Houston J. Math. , 21 (1995) pp. 119–128 |
| [a6] | D.E. Edmunds, H. Triebel, "Logarithmic Sobolev spaces and their applications to spectral theory" Proc. London Math. Soc. , 71 : 3 (1995) pp. 333–371 |
| [a7] | N. Fusco, P.L. Lions, C. Sbordone, "Sobolev imbedding theorems in borderline case" Proc. Amer. Math. Soc. , 124 (1996) pp. 562–565 |
| [a8] | V. Kokilashvili, M. Krbec, "Weighted inequalities in Lorentz and Orlicz spaces" , World Sci. (1991) |
| [a9] | A. Torchinsky, "Interpolation of operators and Orlicz classes" Studia Math. , 59 (1976) pp. 177–207 |
| [a10] | N. Trudinger, "On imbeddings into Orlicz spaces and some applications" J. Math. Mech. , 17 (1967) pp. 473–483 |
Imbedding theorems for Orlicz-Sobolev spaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Imbedding_theorems_for_Orlicz-Sobolev_spaces&oldid=12069