Imbedding of function spaces
A set-theoretic inclusion  of a linear normed space
of a linear normed space  into a linear normed space
into a linear normed space  , for which the following inequality is valid for any
, for which the following inequality is valid for any  :
:
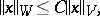 |
where  is a constant which does not depend on
is a constant which does not depend on  . Here,
. Here,  is the norm (semi-norm) of the element
is the norm (semi-norm) of the element  in
in 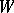 , while
, while  is the norm (semi-norm) of the element
is the norm (semi-norm) of the element  in
in 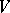 .
.
The identity operator from 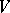 into
into 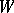 , which assigns to an element
, which assigns to an element 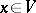 the same element seen as an element of
the same element seen as an element of  , is said to be the imbedding operator of
, is said to be the imbedding operator of  into
into 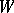 . The imbedding operator is always bounded. If the imbedding operator is a completely-continuous operator, the imbedding of function spaces is said to be compact. Facts on imbedding of function spaces are established by so-called imbedding theorems.
. The imbedding operator is always bounded. If the imbedding operator is a completely-continuous operator, the imbedding of function spaces is said to be compact. Facts on imbedding of function spaces are established by so-called imbedding theorems.
Example. Let 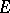 be a Lebesgue-measurable set in the
be a Lebesgue-measurable set in the  -dimensional Euclidean space with finite measure
-dimensional Euclidean space with finite measure 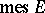 and let
and let  ,
, 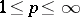 , be the Lebesgue space of measurable functions which are
, be the Lebesgue space of measurable functions which are 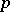 -th power summable over
-th power summable over  with norm
with norm
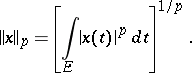 |
Then, if 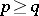 , one has the imbedding
, one has the imbedding 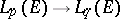 , and
, and
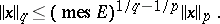 |
Comments
For references cf. Imbedding theorems.
Imbedding of function spaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Imbedding_of_function_spaces&oldid=11516