Illumination problem
The problem of determining the minimum number of directions of pencils of parallel rays, or number of sources, illuminating the whole boundary of a convex body. Let 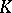 be a convex body in an
be a convex body in an  -dimensional linear space
-dimensional linear space 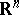 , let
, let 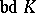 and
and  be respectively its boundary and its interior, and assume that
be respectively its boundary and its interior, and assume that 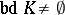 . The best known illumination problems are the following.
. The best known illumination problems are the following.
1) Let 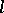 be a certain direction in
be a certain direction in 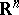 . A point
. A point 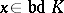 is called illuminated from the outside by the direction
is called illuminated from the outside by the direction 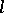 if the straight line passing through
if the straight line passing through  parallel to
parallel to 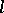 passes through a certain point
passes through a certain point 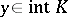 and if the direction of the vector
and if the direction of the vector  coincides with
coincides with  . The minimum number
. The minimum number 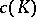 of directions in the space
of directions in the space 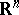 is sought that is sufficient to illuminate the whole set
is sought that is sufficient to illuminate the whole set 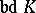 .
.
2) Let  be a point of
be a point of 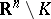 . A point
. A point 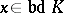 is called illuminated from the outside by the point
is called illuminated from the outside by the point  if the straight line defined by the points
if the straight line defined by the points  and
and  passes through a point
passes through a point 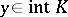 and if the vectors
and if the vectors 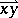 and
and 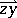 have the same direction. The minimum number
have the same direction. The minimum number  of points from
of points from 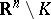 is sought that is sufficient to illuminate the whole set
is sought that is sufficient to illuminate the whole set  .
.
3) Let  be a point of
be a point of 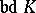 . A point
. A point  is illuminated from within by the point
is illuminated from within by the point 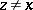 if the straight line defined by the points
if the straight line defined by the points  and
and  passes through a point
passes through a point 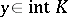 and if the vectors
and if the vectors 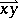 and
and 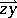 have opposite directions. The minimum number
have opposite directions. The minimum number 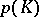 of points from
of points from 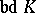 is sought that is sufficient to illuminate the whole set
is sought that is sufficient to illuminate the whole set 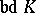 from within.
from within.
4) A system of points 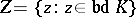 is said to be fixing for
is said to be fixing for  if it possesses the properties: a)
if it possesses the properties: a) 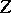 is sufficient to illuminate the whole set
is sufficient to illuminate the whole set 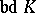 from within; and b)
from within; and b)  does not have any proper subset sufficient to illuminate the set
does not have any proper subset sufficient to illuminate the set 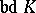 from within. The maximum number
from within. The maximum number 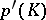 of points of a fixing system is sought for the body
of points of a fixing system is sought for the body 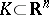 .
.
Problem 1) was proposed in connection with the Hadwiger hypothesis (see [1]): The minimum number of bodies 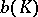 homothetic to a bounded
homothetic to a bounded 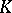 with homothety coefficient
with homothety coefficient 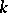 ,
, 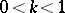 , sufficient for covering
, sufficient for covering 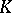 , satisfies the inequality
, satisfies the inequality 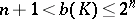 , whereby the value
, whereby the value  characterizes a parallelepiped. For
characterizes a parallelepiped. For 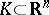 bounded,
bounded, 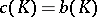 . If
. If 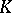 is unbounded, then
is unbounded, then  , and there exist bodies such that
, and there exist bodies such that 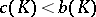 or
or 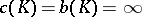 (see [1]).
(see [1]).
Problem 2) was proposed in connection with problem 1). For 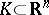 bounded, the equality
bounded, the equality 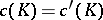 holds. If
holds. If 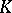 is not bounded, then
is not bounded, then 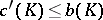 and
and 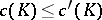 . The number
. The number  for any unbounded
for any unbounded 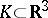 takes one of the values 1, 2, 3, 4,
takes one of the values 1, 2, 3, 4, 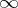 (see [1]).
(see [1]).
The solution of problem 3) takes the form: The number  is defined if and only if
is defined if and only if 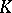 is not a cone. In this case,
is not a cone. In this case,
 |
whereby  characterizes an
characterizes an  -dimensional simplex of the space
-dimensional simplex of the space 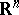 (see [1]).
(see [1]).
For problem 4) (see [2]), it has been conjectured that if 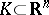 is bounded, the inequality
is bounded, the inequality
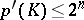 |
holds.
Every illumination problem is closely linked to a special covering of the body 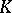 (cf. Covering (of a set)) (see [1]).
(cf. Covering (of a set)) (see [1]).
References
| [1] | V.G. Boltyanskii, P.S. Soltan, "The combinatorial geometry of various classes of convex sets" , Kishinev (1978) (In Russian) |
| [2] | B. Grünbaum, "Fixing systems and inner illumination" Acta Math. Acad. Sci. Hung. , 15 (1964) pp. 161–163 |
Comments
References
| [a1] | R. Schneider, "Boundary structure and curvature of convex bodies" J. Tölke (ed.) J.M. Wills (ed.) , Contributions to geometry , Birkhäuser (1979) pp. 13–59 |
| [a2] | V. [V.G. Boltyanskii] Boltjansky, I. [I. Gokhberg] Gohberg, "Results and problems in combinatorial geometry" , Cambridge Univ. Press (1985) (Translated from Russian) |
Illumination problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Illumination_problem&oldid=18579