Idempotent semi-ring
dioid
A semi-ring with idempotent addition. So, a set  equipped with binary operations
equipped with binary operations  (addition) and
(addition) and  (multiplication) and neutral elements
(multiplication) and neutral elements  and
and  is called an idempotent semi-ring if the following basic properties are valid for all elements
is called an idempotent semi-ring if the following basic properties are valid for all elements  :
:
i)  (idempotent addition);
(idempotent addition);
ii)  ;
;
iii)  ;
;
iv) 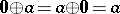 ;
;
v) 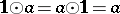 ;
;
vi) 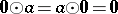 ;
;
vii) 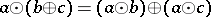 ;
;
viii) 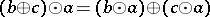 .
.
An idempotent semi-ring 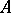 is commutative if
is commutative if  for all
for all 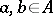 . Different versions of this axiomatics are used, see e.g. [a1], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10]. Idempotent semi-rings are often called dioids, see e.g. [a3], [a9]. The concept of an idempotent semi-ring is a basic concept in idempotent analysis. This concept has many applications in different optimization problems (including dynamic programming), computer science, automata and formal language theory, numerical methods, parallel programming, etc. (cf. also Idempotent algorithm and [a1], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10], [a11]).
. Different versions of this axiomatics are used, see e.g. [a1], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10]. Idempotent semi-rings are often called dioids, see e.g. [a3], [a9]. The concept of an idempotent semi-ring is a basic concept in idempotent analysis. This concept has many applications in different optimization problems (including dynamic programming), computer science, automata and formal language theory, numerical methods, parallel programming, etc. (cf. also Idempotent algorithm and [a1], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10], [a11]).
Example 1.
Let  be the set
be the set 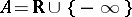 (where
(where 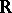 is the field of real numbers) equipped with the operations
is the field of real numbers) equipped with the operations 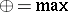 and
and 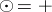 (usual addition); set
(usual addition); set 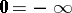 ,
, 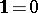 . Similarly, let
. Similarly, let 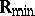 be the set
be the set 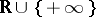 equipped with the operations
equipped with the operations  and
and 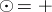 ; in this case
; in this case 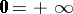 and
and 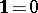 . It is easy to check that
. It is easy to check that 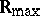 and
and 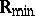 are (isomorphic) commutative idempotent semi-rings.
are (isomorphic) commutative idempotent semi-rings.
Example 2.
Let 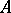 be the set
be the set 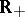 of all non-negative real numbers endowed with the operations
of all non-negative real numbers endowed with the operations 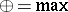 and
and 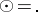 (usual multiplication);
(usual multiplication); 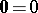 ,
, 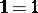 . This idempotent semi-ring is isomorphic to
. This idempotent semi-ring is isomorphic to 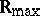 . The isomorphism is given by
. The isomorphism is given by 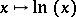 .
.
Example 3.
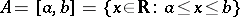 with the operations
with the operations 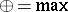 ,
, 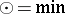 and neutral elements
and neutral elements 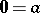 and
and 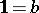 (the cases
(the cases 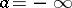 ,
, 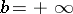 are possible).
are possible).
Example 4.
Let 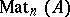 be the set of
be the set of 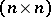 -matrices with entries belonging to an idempotent semi-ring
-matrices with entries belonging to an idempotent semi-ring 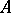 . Then
. Then 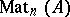 is a non-commutative idempotent semi-ring with respect to matrix addition and matrix multiplication.
is a non-commutative idempotent semi-ring with respect to matrix addition and matrix multiplication.
The Boolean algebra 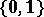 is an example of a finite idempotent semi-ring. There are many other interesting examples of idempotent semi-rings, see e.g. [a1], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10], [a11].
is an example of a finite idempotent semi-ring. There are many other interesting examples of idempotent semi-rings, see e.g. [a1], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10], [a11].
There is a natural partial order on any idempotent semi-ring (as well as on any idempotent semi-group; cf. also Idempotent semi-ring). By definition, 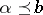 if and only if
if and only if 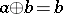 . For this relation, reflexivity is equivalent to idempotency of the (generalized) addition, whereas transitivity, respectively anti-symmetry, follow from associativity, respectively commutativity, of this operation. On
. For this relation, reflexivity is equivalent to idempotency of the (generalized) addition, whereas transitivity, respectively anti-symmetry, follow from associativity, respectively commutativity, of this operation. On 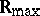 (and also on the semi-rings described in the Examples 2 and 3), this ordering relation coincides with the natural one; on
(and also on the semi-rings described in the Examples 2 and 3), this ordering relation coincides with the natural one; on 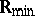 it is the opposite of the natural ordering relation on the real axis. Every element
it is the opposite of the natural ordering relation on the real axis. Every element  in an idempotent semi-ring
in an idempotent semi-ring 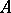 is "non-negative" :
is "non-negative" : 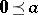 . Indeed,
. Indeed, 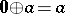 . Similarly, for all
. Similarly, for all 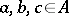 one has
one has 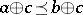 , and
, and  if
if 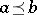 . Using this standard partial order it is possible to define in the usual way the notions of upper and lower bounds, bounded sets,
. Using this standard partial order it is possible to define in the usual way the notions of upper and lower bounds, bounded sets, 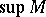 (and
(and 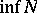 ) for upper- (lower-) bounded sets
) for upper- (lower-) bounded sets 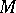 (respectively,
(respectively, 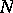 ), etc.
), etc.
If the multiplication in a semi-ring 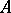 is invertible on
is invertible on 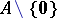 , then
, then 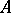 is called a semi-field. For example,
is called a semi-field. For example, 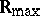 is a semi-field. Idempotent semi-fields and semi-rings with idempotent multiplication are especially interesting.
is a semi-field. Idempotent semi-fields and semi-rings with idempotent multiplication are especially interesting.
References
| [a1] | A.V. Aho, J.E. Hopcroft, J.D. Ullman, "The design and analysis of computer algorithms" , Addison-Wesley (1976) |
| [a2] | B.A. Carré, "Graphs and networks" , Clarendon Press and Oxford Univ. Press (1979) |
| [a3] | M. Gondran, M. Minoux, "Graphes et algorithms" , Ed. Eyrolles (1979; 1988) |
| [a4] | R.A. Cuningham-Green, "Minimax algebra" , Lecture Notes in Economics and Mathematical Systems , 166 , Springer (1979) |
| [a5] | U. Zimmermann, "Linear and combinatorial optimization in ordered algebraic structures" Ann. Discrete Math. , 10 (1981) pp. 1–380 |
| [a6] | "Mathematical aspects of computer engineering" V.P. Maslov (ed.) K.A. Volosov (ed.) , MIR (1988) (In Russian) |
| [a7] | "Idempotent analysis" V.P. Maslov (ed.) S.N. Samborskii (ed.) , Amer. Math. Soc. (1992) (In Russian) |
| [a8] | V.N. Kolokoltsov, V.P. Maslov, "Idempotent analysis and applications" , Kluwer Acad. Publ. (1996) (In Russian) |
| [a9] | F.L. Baccelli, G. Cohen, G.J. Olsder, J.-P. Quadrat, "Synchronization and linearity: an algebra for discrete event systems" , Wiley (1992) |
| [a10] | J.S. Golan, "The theory of semirings with applications in mathematics and theoretical computer science" , Pitman monographs and surveys in pure and applied mathematics , 54 , Longman (1992) |
| [a11] | "Idempotency" J. Gunawardena (ed.) , Publ. I. Newton Institute , Cambridge Univ. Press (in press) |
Idempotent semi-ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Idempotent_semi-ring&oldid=16503