Hyperspace
over a topological space 
A space whose points are the elements of some family  of subsets of
of subsets of  with some topology.
with some topology.  is usually a ring of sets, but this is not assumed in advance.
is usually a ring of sets, but this is not assumed in advance.
Example.  is the hyperspace of all subsets of a space
is the hyperspace of all subsets of a space  ; a basis for the topology is formed by the sets
; a basis for the topology is formed by the sets  provided that
provided that  is closed in
is closed in 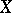 ,
,  is open in
is open in 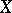 and
and  .
.
The most frequently occurring hyperspace is  . It consists of all closed subsets of a topological space
. It consists of all closed subsets of a topological space 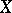 ; a sub-base of the exponential topology on
; a sub-base of the exponential topology on  is formed by
is formed by  and
and  , where
, where  and
and  are open in
are open in  and
and  runs through
runs through  . Topologies in the following hyperspaces are defined in the same manner: on the set
. Topologies in the following hyperspaces are defined in the same manner: on the set 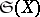 of all compact subsets of a space
of all compact subsets of a space  ; on the set
; on the set  of all finite subsets of a space
of all finite subsets of a space 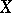 ; on the set
; on the set  of all subcontinua (connected compacta) of a continuum
of all subcontinua (connected compacta) of a continuum  , etc. These spaces may be regarded as subspaces of the hyperspace
, etc. These spaces may be regarded as subspaces of the hyperspace 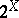 endowed with the exponential topology. If
endowed with the exponential topology. If 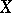 is a uniform space, then the set
is a uniform space, then the set 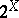 has a natural uniform structure; the uniform space obtained in this way is denoted by
has a natural uniform structure; the uniform space obtained in this way is denoted by  . If
. If  is compact, then the hyperspaces
is compact, then the hyperspaces 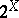 ,
,  and
and  are all homeomorphic and are compact. If
are all homeomorphic and are compact. If  is a compact metrizable space, so is
is a compact metrizable space, so is  . If
. If 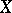 is a continuum, so are
is a continuum, so are  and
and  .
.
References
| [1] | K. Kuratowski, "Topology" , 2 , Acad. Press (1968) (Translated from French) |
| [2] | E. Michael, "Topologies on spaces of subsets" Trans. Amer. Math. Soc. , 71 (1951) pp. 152–182 |
| [3] | V.I. Ponomarev, "A new space of closed sets and many-valued continuous maps of bicompacts" Mat. Sb. , 48 (90) : 2 (1959) pp. 191–212 (In Russian) |
Comments
The exponential topology is commonly called the Vietoris topology, in honour of L. Vietoris who introduced it in 1922 [a1]. However, it made little impact on topology for 20 years, until it was rediscovered by O. Frink [a2] and by E. Michael [2]. If  is a compact metric space, then the Vietoris topology on
is a compact metric space, then the Vietoris topology on  is induced by the Hausdorff metric. For general accounts of hyperspace theory, see [a3] and [a4].
is induced by the Hausdorff metric. For general accounts of hyperspace theory, see [a3] and [a4].
On  one frequently considers the topology generated by the family
one frequently considers the topology generated by the family  , where
, where 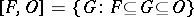 . Thus topologized
. Thus topologized  is called the Pixley–Roy hyperspace of
is called the Pixley–Roy hyperspace of  . It is often used in the construction of counterexamples, see [a5].
. It is often used in the construction of counterexamples, see [a5].
References
| [a1] | L. Vietoris, "Bereiche zweiter Ordnung" Monatsh. Math. Physik , 32 (1922) pp. 258–280 |
| [a2] | O. Frink, "Topology in lattices" Trans. Amer. Math. Soc. , 51 (1942) pp. 569–582 |
| [a3] | S.B. Nadler, "Hyperspaces of sets" , M. Dekker (1978) |
| [a4] | B.L. McAllister, "Hyperspaces and multifunctions, the first half century" Nieuw Arch. Wisk. (3) , 26 (1978) pp. 309–329 |
| [a5] | E.K. van Douwen, "The Pixley–Roy topology on spaces of subsets" G.M. Reed (ed.) , Set-Theoretic Topology , Acad. Press (1977) pp. 111–134 |
Hyperspace. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperspace&oldid=18550