Hyperplane

in a vector space over a field

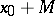The image (under a translation) of a vector subspace with one-dimensional quotient space , i.e. a set of the form for a certain . If , the hyperplane is sometimes called homogeneous. A subset is a hyperplane if and only if

(*)

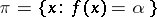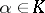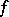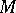for and a certain non-zero linear functional . Here, and are defined by up to a common factor .

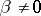In a topological vector space any hyperplane is either closed or is everywhere dense; 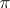as defined by formula is closed if and only if the functional 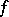is continuous.