Hyperhomology functor
A series of functors 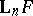 on the category of complexes connected with some functor
on the category of complexes connected with some functor 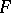 . In fact, let
. In fact, let  be a covariant additive functor from an Abelian category
be a covariant additive functor from an Abelian category 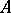 with a sufficient number of projective objects into an Abelian category
with a sufficient number of projective objects into an Abelian category 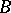 . Further, let
. Further, let 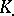 be a chain complex with values in
be a chain complex with values in 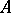 and let
and let 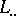 be a Cartan–Eilenberg resolution of
be a Cartan–Eilenberg resolution of 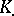 , consisting of projective objects. Then the bicomplex
, consisting of projective objects. Then the bicomplex 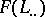 determines the homology groups
determines the homology groups 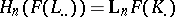 and two spectral sequences (cf. Spectral sequence) converging to them with initial terms
and two spectral sequences (cf. Spectral sequence) converging to them with initial terms
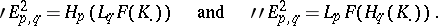 |
These homology groups and spectral sequences depend functorially on 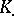 and are known, respectively, as the hyperhomology functors for
and are known, respectively, as the hyperhomology functors for 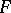 and the spectral hyperhomology functors for
and the spectral hyperhomology functors for 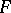 . The hyperhomology functor
. The hyperhomology functor 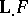 is a homology functor on the category of complexes in the following important cases: when
is a homology functor on the category of complexes in the following important cases: when 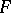 commutes with inductive limits; when the objects in the category
commutes with inductive limits; when the objects in the category 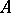 have projective resolutions of length
have projective resolutions of length 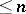 ; or when it is considered on the category of complexes with positive degrees.
; or when it is considered on the category of complexes with positive degrees.
Hypercohomology functors are defined dually.
References
| [1] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [2] | A. Grothendieck, "Sur quelques points d'algèbre homologique" Tohoku Math. J. , 9 (1957) pp. 119–221 |
Hyperhomology functor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperhomology_functor&oldid=12890