Hypergraph
A generalization of the concept of a graph. A hypergraph is defined by a set 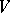 , whose elements are known as vertices, and by a family
, whose elements are known as vertices, and by a family 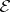 of subsets of
of subsets of 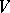 , known as edges or hyperedges. A hypergraph is denoted by
, known as edges or hyperedges. A hypergraph is denoted by 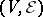 . The concept of a hypergraph is a variant of the familiar concepts of a complex, a block design and a network.
. The concept of a hypergraph is a variant of the familiar concepts of a complex, a block design and a network.
Two vertices of a hypergraph are said to be adjacent if there exists an edge containing these vertices. A vertex  and an edge
and an edge 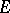 of a hypergraph are said to be incident if
of a hypergraph are said to be incident if 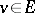 . A hypergraph
. A hypergraph 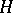 with
with  vertices and
vertices and 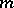 edges may be defined by an incidence matrix, i.e. by the matrix
edges may be defined by an incidence matrix, i.e. by the matrix 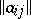 of dimension
of dimension 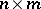 in which the columns correspond to the edges while the rows correspond to the vertices of the hypergraph, and where
in which the columns correspond to the edges while the rows correspond to the vertices of the hypergraph, and where
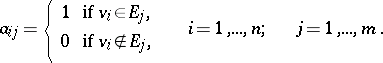 |
It is possible to assign to each matrix 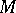 consisting of zeros and ones a hypergraph for which
consisting of zeros and ones a hypergraph for which 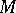 is the incidence matrix. The hypergraph
is the incidence matrix. The hypergraph 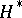 is called the dual of the hypergraph
is called the dual of the hypergraph 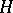 if the incidence matrix of
if the incidence matrix of 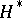 is obtained by transposing the incidence matrix of
is obtained by transposing the incidence matrix of 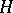 . The number of edges of a hypergraph
. The number of edges of a hypergraph 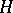 that are incident to a given vertex is called the degree of the vertex. The degree of an edge is the number of vertices of the hypergraph incident to this edge. A hypergraph
that are incident to a given vertex is called the degree of the vertex. The degree of an edge is the number of vertices of the hypergraph incident to this edge. A hypergraph 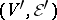 is called a subhypergraph of a hypergraph
is called a subhypergraph of a hypergraph 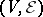 if
if 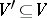 ,
, 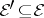 , and if a vertex
, and if a vertex  from
from  and an edge
and an edge 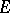 from
from 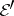 are incident in the hypergraph
are incident in the hypergraph 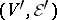 if and only if they are incident in the hypergraph
if and only if they are incident in the hypergraph 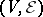 .
.
A hypergraph may be represented in a plane by identifying the vertices of the hypergraph with points of the plane and by identifying the edges with connected domains containing the vertices incident with these edges. For instance, it is possible to represent the hypergraph 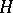 with set of vertices
with set of vertices 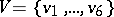 and family of edges
and family of edges
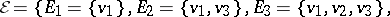 |
 |
in a plane, as shown in the figure.
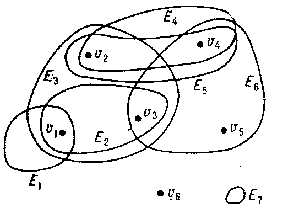
Figure: h048470a
A hypergraph  may be represented by a bipartite graph (cf. Graph, bipartite)
may be represented by a bipartite graph (cf. Graph, bipartite) 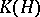 in which the vertices of one part
in which the vertices of one part 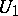 correspond to the vertices of the hypergraph, while the vertices of the other part
correspond to the vertices of the hypergraph, while the vertices of the other part 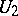 correspond to the edges of
correspond to the edges of 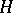 . Two vertices
. Two vertices 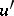 from
from 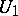 and
and 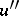 from
from 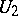 will be connected by an edge in the graph
will be connected by an edge in the graph 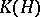 if the vertex of the hypergraph corresponding to
if the vertex of the hypergraph corresponding to 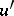 is incident to the edge of the hypergraph corresponding to
is incident to the edge of the hypergraph corresponding to 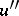 . A hypergraph is a graph if each of its edges has degree two. An important special case of the concept of a "hypergraph" is that of a matroid. Many concepts in the theory of graphs, such as connectedness, planarity, the chromatic number, and the external and internal stability numbers, may be applied to hypergraphs, as may many theorems that are applicable to graphs.
. A hypergraph is a graph if each of its edges has degree two. An important special case of the concept of a "hypergraph" is that of a matroid. Many concepts in the theory of graphs, such as connectedness, planarity, the chromatic number, and the external and internal stability numbers, may be applied to hypergraphs, as may many theorems that are applicable to graphs.
References
| [1] | A.A. Zykov, "Hypergraphs" Russian Math. Surveys , 29 : 6 (1974) pp. 89–156 Uspekhi Mat. Nauk , 29 : 6 (1974) pp. 80–154 |
| [2] | C. Berge, "Graphs and hypergraphs" , North-Holland (1973) (Translated from French) |
Hypergraph. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypergraph&oldid=11526