Hypergeometric series
Gauss series
A series of the form
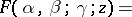 |
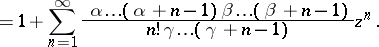 |
Such a series is meaningful if 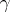 is not equal to zero or to a negative integer; it converges for
is not equal to zero or to a negative integer; it converges for 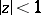 . If, in addition,
. If, in addition, 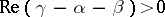 , it also converges for
, it also converges for 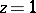 . In such a case the Gauss formula
. In such a case the Gauss formula
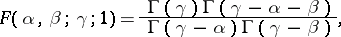 |
where 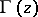 is the gamma-function, holds. An analytic function defined with the aid of a hypergeometric series is said to be a hypergeometric function.
is the gamma-function, holds. An analytic function defined with the aid of a hypergeometric series is said to be a hypergeometric function.
A generalized hypergeometric series is a series of the form
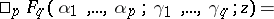 |
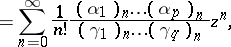 |
where 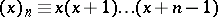 . If this notation is used, the series
. If this notation is used, the series
is written as 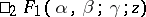 .
.
Comments
Generalized hypergeometric series can be characterized as power series 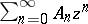 such that
such that 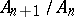 is a rational function of
is a rational function of  . An analogous characterization for series in two variables was given by J. Horn. This yields a class of power series in two variables which includes the various Appell's hypergeometric series, cf. [a1].
. An analogous characterization for series in two variables was given by J. Horn. This yields a class of power series in two variables which includes the various Appell's hypergeometric series, cf. [a1].
Basic hypergeometric series can be characterized as power series 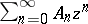 such that
such that 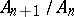 is a rational function of
is a rational function of 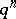 , where
, where 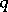 is a fixed complex number not equal to 0 or 1. Such series have the form
is a fixed complex number not equal to 0 or 1. Such series have the form
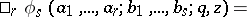 |
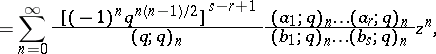 |
where  . See [a2].
. See [a2].
Hypergeometric functions of matrix argument have also been studied, cf. [a3].
References
| [a1] | P. Appell, M.J. Kampé de Fériet, "Fonctions hypergéométriques et hypersphériques: Polynômes d'Hermite" , Gauthier-Villars (1926) |
| [a2] | G. Gasper, M. Rahman, "Basic hypergeometric series" , Cambridge Univ. Press (1989) |
| [a3] | K. Gross, D. Richards, "Special functions of matrix argument I" Trans. Amer. Math. Soc. , 301 (1987) pp. 781–811 |
Hypergeometric series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypergeometric_series&oldid=11231