Hypergeometric distribution

The probability distribution defined by the formula

(*)

where 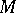, 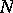and are non-negative integers and 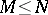, 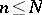(here is the binomial coefficient, sometimes also denoted by 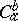). The hypergeometric distribution is usually connected with sampling without replacement: Formula (*) gives the probability of obtaining exactly "marked" elements as a result of randomly sampling items from a population containing 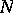elements out of which 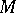elements are "marked" and 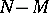are "unmarked" . The probability (*) is defined only for

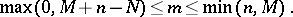However, the definition (*) may be used for all 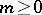, because one may assume that 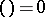if 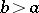, so that the equality 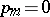may be understood as the impossibility of obtaining 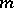"marked" elements of the sample. The sum of the values 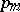, extended to include the entire sample space, is one. If one puts 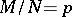, then (*) may be written as follows:

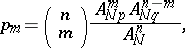where

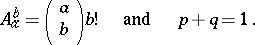If 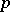is constant and 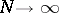, the binomial approximation

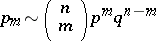results. The expectation of the hypergeometric distribution is independent of 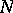and coincides with the expectation 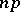of the corresponding binomial distribution. The variance of the hypergeometric distribution,

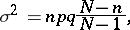is smaller than that of the binomial law, 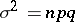. If 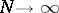, the moments of the hypergeometric distribution of any order tend to the corresponding values of the moments of the binomial distribution. The generating function of the hypergeometric distribution has the form

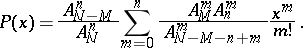The series on the right-hand side of this equation represents the hypergeometric function 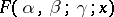, where 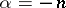, 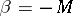and 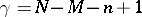(hence the name of the distribution). The probability (*) and the corresponding distribution function have been tabulated for a wide range of values.

References

[1]	G.I. Lieberman, D.B. Owen, "Tables of the hypergeometric probability distribution" , Stanford Univ. Press (1961)
[2]	D.B. Owen, "Handbook of statistical tables" , Addison-Wesley (1962)
[3]	L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)
[4]	W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1970)