Hyperbolic point
A hyperbolic point of a surface is a point at which the osculating paraboloid is a hyperbolic paraboloid. At a hyperbolic point the Dupin indicatrix is given by a pair of conjugate hyperbolas.
Comments
At a hyperbolic point the surface has negative Gaussian curvature, and conversely: If a surface has negative Gaussian curvature at a point, that point is hyperbolic.
References
| [a1] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) |
A hyperbolic point of a dynamical system is a point 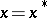 in the domain of definition of a system
in the domain of definition of a system
 | (*) |
such that 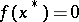 , while the matrix
, while the matrix 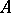 , which is equal to the value of
, which is equal to the value of 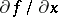 at
at 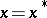 , has
, has 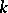 eigen values with positive real part and
eigen values with positive real part and 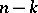 eigen values with negative real part,
eigen values with negative real part, 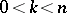 . In a neighbourhood of a hyperbolic point there exists an
. In a neighbourhood of a hyperbolic point there exists an 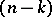 -dimensional invariant surface
-dimensional invariant surface 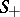 , constituted by solutions of (*) which, as
, constituted by solutions of (*) which, as 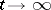 , asymptotically approach
, asymptotically approach 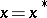 , as well as a
, as well as a 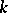 -dimensional invariant surface
-dimensional invariant surface 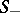 , formed by the solutions of (*) which asymptotically approach
, formed by the solutions of (*) which asymptotically approach 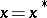 as
as 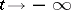 . The behaviour of the trajectories of (*) in a sufficiently small neighbourhood of a hyperbolic point may be described by means of the following theorem [4]: There exists a homeomorphism of some neighbourhood of a hyperbolic point onto some neighbourhood of the point
. The behaviour of the trajectories of (*) in a sufficiently small neighbourhood of a hyperbolic point may be described by means of the following theorem [4]: There exists a homeomorphism of some neighbourhood of a hyperbolic point onto some neighbourhood of the point 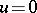 ,
, 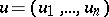 , which converts the trajectories of (*) into trajectories of the linear system
, which converts the trajectories of (*) into trajectories of the linear system 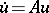 .
.
For a diffeomorphism with a fixed point, a hyperbolic point is defined by the absence of eigen values of modulus one in the linear part of the diffeomorphism at the fixed point under consideration. Thus, a hyperbolic point of the system (*) remains a hyperbolic point of the diffeomorphism generated by a shift along a trajectory of the system (*).
References
| [1a] | H. Poincaré, "Mémoire sur les courbes definiés par une équation différentielle" J. de Math. , 7 (1881) pp. 375–422 |
| [1b] | H. Poincaré, "Mémoire sur les courbes definiés par une équation différentielle" J. de Math. , 8 (1882) pp. 251–296 |
| [1c] | H. Poincaré, "Mémoire sur les courbes definiés par une équation différentielle" J. de Math. , 1 (1885) pp. 167–244 |
| [1d] | H. Poincaré, "Mémoire sur les courbes difiniés par une équation différentielle" J. de Math. , 2 (1886) pp. 151–217 |
| [2] | A.M. [A.M. Lyapunov] Liapunoff, "Problème général de la stabilité du mouvement" , Princeton Univ. Press (1947) (Translated from Russian) (Reprint: Kraus, 1950) |
| [3] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [4] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
V.K. Mel'nikov
Comments
Often, an invariant point in the system (*) is said to be hyperbolic whenever the matrix 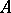 has no eigen values with real part zero (i.e., in the above also
has no eigen values with real part zero (i.e., in the above also 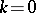 and
and 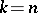 are admitted). See, e.g., [a1].
are admitted). See, e.g., [a1].
References
| [a1] | M.C. Irwin, "Smooth dynamical systems" , Acad. Press (1980) |
Hyperbolic point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_point&oldid=18331