Hyperbolic partial differential equation
at a given point 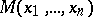
A partial differential equation for which the Cauchy problem is uniquely solvable for initial data specified in a neighbourhood of  on any non-characteristic surface (cf. Characteristic surface). In particular, a partial differential equation for which the normal cone has no imaginary zones is a hyperbolic partial differential equation. The differential equation
on any non-characteristic surface (cf. Characteristic surface). In particular, a partial differential equation for which the normal cone has no imaginary zones is a hyperbolic partial differential equation. The differential equation
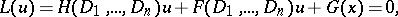 | (*) |
where 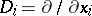 (
( ),
), 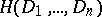 is a homogeneous polynomial of degree
is a homogeneous polynomial of degree  , while the polynomial
, while the polynomial 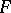 is of lower degree than
is of lower degree than 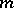 , is a hyperbolic partial differential equation if its characteristic equation
, is a hyperbolic partial differential equation if its characteristic equation
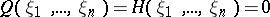 |
has 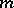 different real solutions with respect to one of the variables
different real solutions with respect to one of the variables 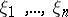 , the remaining ones being fixed. Any equation (*) of the first order
, the remaining ones being fixed. Any equation (*) of the first order 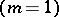 with real coefficients is a hyperbolic partial differential equation. A second-order equation
with real coefficients is a hyperbolic partial differential equation. A second-order equation
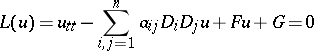 |
is hyperbolic if the quadratic form
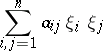 |
is positive definite.
Comments
The special variable among the 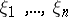 such that
such that 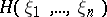 has
has 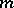 different real solutions for each set of fixed values of the other
different real solutions for each set of fixed values of the other 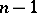 is often taken to be
is often taken to be 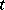 (time). One speaks then of a (strictly) hyperbolic equation or an equation of (strictly) hyperbolic type with respect to the
(time). One speaks then of a (strictly) hyperbolic equation or an equation of (strictly) hyperbolic type with respect to the 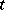 -direction. More generally one considers hyperbolicity with respect to a vector
-direction. More generally one considers hyperbolicity with respect to a vector 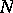 [a1].
[a1].
A polynomial 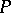 of degree
of degree 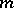 with principal part
with principal part 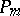 is called hyperbolic with respect to the real vector
is called hyperbolic with respect to the real vector 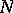 if
if 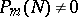 and there exists a number
and there exists a number 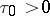 such that
such that
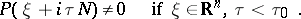 |
If 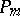 is such that
is such that 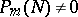 and
and 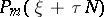 has only simple real roots for every real
has only simple real roots for every real 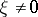 , then
, then 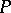 is said to be strictly hyperbolic or hyperbolic in the sense of Petrovskii.
is said to be strictly hyperbolic or hyperbolic in the sense of Petrovskii.
The Cauchy problem for a constant-coefficient differential operator 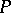 with data on a non-characteristic plane is well posed for arbitrary lower-order terms if and only if
with data on a non-characteristic plane is well posed for arbitrary lower-order terms if and only if 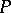 is strictly hyperbolic. For a discussion of similar matters for polynomials
is strictly hyperbolic. For a discussion of similar matters for polynomials 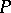 with variable coefficients cf. [a2].
with variable coefficients cf. [a2].
For a system of higher-order linear partial differential equations
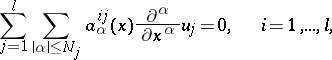 |
where 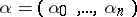 , is a hyperbolic system of partial differential equations in the sense of Petrovskii if the determinant
, is a hyperbolic system of partial differential equations in the sense of Petrovskii if the determinant
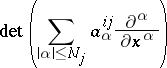 |
calculated in the ring of differential operators is a hyperbolic polynomial in the sense of Petrovskii (as a polynomial of degree 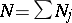 ). The Cauchy problem for a system that is hyperbolic in this sense is well posed [a3], [a4].
). The Cauchy problem for a system that is hyperbolic in this sense is well posed [a3], [a4].
Instead of strictly hyperbolic one also finds the term strongly hyperbolic and instead of hyperbolic also weakly hyperbolic (which is therefore the case in which the lower-order terms of 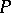 do matter).
do matter).
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) pp. Chapt. XII |
| [a2] | L.V. Hörmander, "The analysis of linear partial differential operators" , III , Springer (1985) pp. Chapt. XXIII |
| [a3] | I.G. Petrovskii, "Ueber das Cauchysche Problem für Systeme von partiellen Differentialgleichungen" Mat. Sb. (N.S.) , 2(44) (1937) pp. 815–870 |
| [a4] | S. Mizohata, "The theory of partial differential equations" , Cambridge Univ. Press (1973) (Translated from Japanese) |
| [a5] | J. Chaillou, "Hyperbolic differential polynomials" , Reidel (1979) |
| [a6] | J. Chazarain, "Opérateurs hyperboliques à characteristique de multiplicité constante" Ann. Inst. Fourier , 24 (1974) pp. 173–202 |
| [a7] | L. Gårding, "Linear hyperbolic equations with constant coefficients" Acta Math. , 85 (1951) pp. 1–62 |
| [a8] | O.A. Oleinik, "On the Cauchy problem for weakly hyperbolic equations" Comm. Pure Appl. Math. , 23 (1970) pp. 569–586 |
Hyperbolic partial differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_partial_differential_equation&oldid=16785