Hyper-elliptic integral
The special case of an Abelian integral
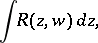 | (1) |
where  is a rational function in variables
is a rational function in variables  ,
,  which are related by an algebraic equation of special type:
which are related by an algebraic equation of special type:
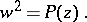 | (2) |
Here  is a polynomial of degree
is a polynomial of degree  without multiple roots. For
without multiple roots. For  one obtains elliptic integrals (cf. Elliptic integral), while the cases
one obtains elliptic integrals (cf. Elliptic integral), while the cases  are sometimes denoted as ultra-elliptic.
are sometimes denoted as ultra-elliptic.
Equation (2) corresponds to a two-sheeted compact Riemann surface 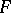 of genus
of genus 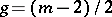 if
if 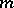 is even, and of genus
is even, and of genus 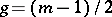 if
if 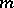 is odd; thus, for hyper-elliptic integrals
is odd; thus, for hyper-elliptic integrals 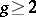 . The functions
. The functions  ,
, 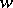 , and hence also
, and hence also 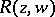 , are single-valued on
, are single-valued on 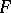 . The integral (1), considered as a definite integral, is given on
. The integral (1), considered as a definite integral, is given on 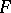 as a curvilinear integral of an analytic function taken along some rectifiable path
as a curvilinear integral of an analytic function taken along some rectifiable path  and, in general, the value of the integral (1) is completely determined by a specification of the initial and final points of
and, in general, the value of the integral (1) is completely determined by a specification of the initial and final points of  alone.
alone.
As in the general case of Abelian integrals, any hyper-elliptic integral can be expressed as a linear combination of elementary functions and canonical hyper-elliptic integrals of the first, second and third kinds, having their specific forms. Thus, a normal hyper-elliptic integral of the first kind is a linear combination of hyper-elliptic integrals of the first kind
 |
where  ,
,  , is the simplest basis of Abelian differentials (cf. Abelian differential) of the first kind for the case of a hyper-elliptic surface
, is the simplest basis of Abelian differentials (cf. Abelian differential) of the first kind for the case of a hyper-elliptic surface  . Explicit expressions for Abelian differentials of the second and third kinds and for the corresponding hyper-elliptic integrals can also be readily computed [2]. Basically, the theory of hyper-elliptic integrals coincides with the general theory of Abelian integrals.
. Explicit expressions for Abelian differentials of the second and third kinds and for the corresponding hyper-elliptic integrals can also be readily computed [2]. Basically, the theory of hyper-elliptic integrals coincides with the general theory of Abelian integrals.
All rational functions 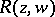 of variables
of variables  and
and 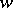 satisfying equation (2) above form a hyper-elliptic field of algebraic functions, of genus
satisfying equation (2) above form a hyper-elliptic field of algebraic functions, of genus 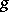 . Any compact Riemann surface of genus
. Any compact Riemann surface of genus 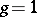 or
or 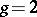 has an elliptic or hyper-elliptic field, respectively. However, if
has an elliptic or hyper-elliptic field, respectively. However, if 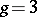 or higher, there exist compact Riemann surfaces
or higher, there exist compact Riemann surfaces 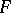 of a complicated structure for which this assertion is no longer true.
of a complicated structure for which this assertion is no longer true.
References
| [1] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt. 10 |
| [2] | R. Nevanlinna, "Uniformisierung" , Springer (1953) pp. Chapt.5 |
| [3] | K. Neumann, "Vorlesungen uber Riemanns Theorie der Abelschen Integrale" , Leipzig (1884) |
Hyper-elliptic integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyper-elliptic_integral&oldid=13571