Hyper-elliptic curve
A non-singular projective model of the affine curve 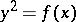 , where
, where 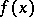 is a polynomial without multiple roots of odd degree
is a polynomial without multiple roots of odd degree  (the case of even degree
(the case of even degree 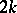 may be reduced to that of odd degree
may be reduced to that of odd degree 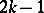 ). The field of functions on a hyper-elliptic curve (a field of hyper-elliptic functions) is a quadratic extension of the field of rational functions; in this sense it is the simplest field of algebraic functions except for the field of rational functions. Hyper-elliptic curves are distinguished by the condition of the existence of a one-dimensional linear series
). The field of functions on a hyper-elliptic curve (a field of hyper-elliptic functions) is a quadratic extension of the field of rational functions; in this sense it is the simplest field of algebraic functions except for the field of rational functions. Hyper-elliptic curves are distinguished by the condition of the existence of a one-dimensional linear series 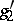 of divisors of degree 2, defining a morphism of order 2 of the hyper-elliptic curve onto the projective straight line. The genus of a hyper-elliptic curve is
of divisors of degree 2, defining a morphism of order 2 of the hyper-elliptic curve onto the projective straight line. The genus of a hyper-elliptic curve is 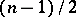 , so that, for various odd
, so that, for various odd  , hyper-elliptic curves are birationally inequivalent. For
, hyper-elliptic curves are birationally inequivalent. For 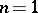 one obtains the projective straight line; for
one obtains the projective straight line; for 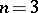 an elliptic curve is obtained. Traditionally, curves of genus 0 and 1 are not called hyper-elliptic curves. The fractions of regular differential forms generate a subfield of genus 0 on a hyper-elliptic curve of genus
an elliptic curve is obtained. Traditionally, curves of genus 0 and 1 are not called hyper-elliptic curves. The fractions of regular differential forms generate a subfield of genus 0 on a hyper-elliptic curve of genus 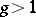 ; this property is a complete characterization of hyper-elliptic curves.
; this property is a complete characterization of hyper-elliptic curves.
References
| [1] | C. Chevalley, "Introduction to the theory of algebraic functions of one variable" , Amer. Math. Soc. (1951) |
| [2] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 |
| [3] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
Comments
The definition given in the main article (first sentence) is only valid in characteristic not equal to 2. In general, a hyper-elliptic curve can be defined as a double covering (cf. also Covering surface) of a rational curve.
References
| [a1] | E. Arbarello, M. Cornalba, P.A. Griffiths, J.E. Harris, "Geometry of algebraic curves" , 1 , Springer (1985) |
Hyper-elliptic curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyper-elliptic_curve&oldid=16119