Hurwitz transformation
The general framework for defining and studying the Hurwitz transformations is that of the Cayley–Dickson algebras (cf. also Cayley–Dickson algebra). Familiar examples of Cayley–Dickson algebras are:
 and
and  , the algebras of ordinary and hyperbolic complex numbers, respectively;
, the algebras of ordinary and hyperbolic complex numbers, respectively;
 and
and  , the algebras of ordinary (or Hamilton) and hyperbolic quaternions, respectively;
, the algebras of ordinary (or Hamilton) and hyperbolic quaternions, respectively;
 and
and  , the algebras of ordinary (or Cayley) and hyperbolic octonions, respectively. Higher-dimensional Cayley–Dickson algebras over the real field
, the algebras of ordinary (or Cayley) and hyperbolic octonions, respectively. Higher-dimensional Cayley–Dickson algebras over the real field  are denoted by
are denoted by  , where
, where  is a
is a 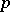 -tuple
-tuple  with
with 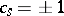 (
(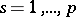 ). Such a
). Such a 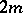 -dimensional algebra
-dimensional algebra 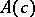 , with
, with  , may be constructed from an
, may be constructed from an 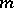 -dimensional Cayley–Dickson algebra by a "doubling" process [a1], [a2], [a3]. (This process generalizes
-dimensional Cayley–Dickson algebra by a "doubling" process [a1], [a2], [a3]. (This process generalizes 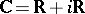 .) For fixed
.) For fixed 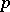 , the algebra
, the algebra 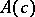 with
with 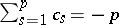 corresponds to ordinary (or elliptic) hypercomplex numbers (cf. also Hypercomplex number), while the
corresponds to ordinary (or elliptic) hypercomplex numbers (cf. also Hypercomplex number), while the 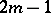 other algebras
other algebras 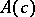 with
with 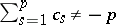 correspond to hyperbolic hypercomplex numbers. The Cayley–Dickson algebra
correspond to hyperbolic hypercomplex numbers. The Cayley–Dickson algebra 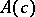 is referred to as normed or pseudo-normed according to whether the metric
is referred to as normed or pseudo-normed according to whether the metric
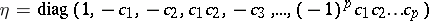 |
is Euclidean or pseudo-Euclidean (cf. also Euclidean space; Pseudo-Euclidean space). For each algebra 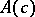 there exist
there exist 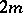 anti-involutions
anti-involutions 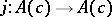 :
: 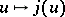 , (the mapping
, (the mapping 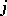 satisfies
satisfies  and
and  ). One of the anti-involutions is the mapping
). One of the anti-involutions is the mapping
 |
 |
the remaining  anti-involutions correspond to anti-involutions of type
anti-involutions correspond to anti-involutions of type 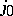 on the various
on the various 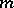 -dimensional Cayley–Dickson subalgebras of
-dimensional Cayley–Dickson subalgebras of 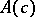 .
.
An element 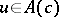 has
has  real components
real components 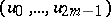 ; these define a vector in
; these define a vector in 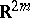 and can thus be associated with a column vector
and can thus be associated with a column vector 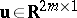 . From the product
. From the product 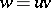 of two elements
of two elements 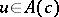 and
and 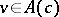 , an
, an 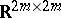 (generalized) Hurwitz matrix
(generalized) Hurwitz matrix 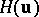 is defined via
is defined via  .
.
The application
 | (a1) |
where  with
with  (
(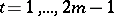 ), defines a mapping
), defines a mapping 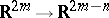 , called Hurwitz transformation and denoted by
, called Hurwitz transformation and denoted by 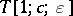 . The row vector
. The row vector 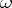 consists of:
consists of:
i) 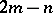 total differentials, leading to a vector
total differentials, leading to a vector 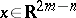 ;
;
ii)  one-forms
one-forms  (when
(when 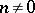 ) which are not total differentials and which are taken to be equal to zero to account for the non-bijectivity of the mapping
) which are not total differentials and which are taken to be equal to zero to account for the non-bijectivity of the mapping 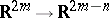 :
:  . The integer
. The integer  ,
, 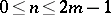 , depends on
, depends on  . The various possibilities for
. The various possibilities for  are:
are:
1)  is the unit
is the unit 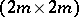 -matrix;
-matrix;
2)  is such that
is such that  (
(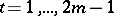 ) and thus corresponds to the anti-involution
) and thus corresponds to the anti-involution 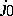 of
of 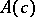 (
( if and only if
if and only if 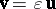 );
);
3) 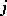 corresponds to one of the
corresponds to one of the 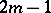 remaining anti-involutions of
remaining anti-involutions of 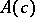 ;
;
4)  is a matrix not listed in the other cases. Equation (a1) defines the components of
is a matrix not listed in the other cases. Equation (a1) defines the components of  as quadratic functions of the components of
as quadratic functions of the components of  . For
. For 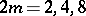 , the vector
, the vector  may also be generated from the product
may also be generated from the product 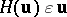 that produces a column vector, with
that produces a column vector, with  vanishing entries and
vanishing entries and 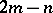 non-vanishing entries, corresponding to
non-vanishing entries, corresponding to  .
.
Another type of Hurwitz transformation, denoted by 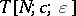 , is formally obtained by replacing
, is formally obtained by replacing 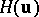 in (a1) or in
in (a1) or in 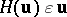 by
by 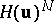 with
with 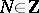 . This leads to non-quadratic transformations [a4].
. This leads to non-quadratic transformations [a4].
The cases 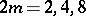 deserve special attention, since they correspond to the Hurwitz factorization problem (the situations addressed in [a5] concern
deserve special attention, since they correspond to the Hurwitz factorization problem (the situations addressed in [a5] concern 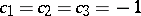 for
for 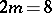 ,
, 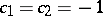 for
for 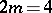 and
and 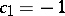 for
for 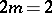 ). In these cases, the
). In these cases, the 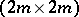 -matrix
-matrix 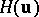 satisfies
satisfies
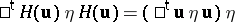 |
and may be written in terms of elements of a Clifford algebra of degree 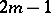 . As a consequence, the factorization property
. As a consequence, the factorization property
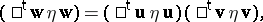 |
for 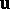 and
and  fixed, is satisfied by
fixed, is satisfied by 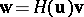 for
for 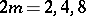 .
.
The geometric and group-theoretical properties of the transformations 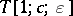 for
for 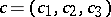 ,
, 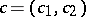 and
and 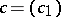 are well known. From the geometrical point of view, they correspond to fibrations on spheres and hyperboloids [a3], [a6]. From the point of view of group theory, they are associated to Lie algebras under constraints [a7].
are well known. From the geometrical point of view, they correspond to fibrations on spheres and hyperboloids [a3], [a6]. From the point of view of group theory, they are associated to Lie algebras under constraints [a7].
Some typical examples of 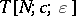 are as follows. The case
are as follows. The case 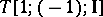 , where
, where  is the unit
is the unit 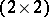 -matrix, corresponds to the Levi-Civita transformation
-matrix, corresponds to the Levi-Civita transformation 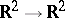 used in the restricted three-body problem of classical mechanics [a8]. The case
used in the restricted three-body problem of classical mechanics [a8]. The case 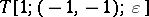 , where
, where 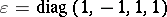 , corresponds to the Kustaanheimo–Stiefel transformation
, corresponds to the Kustaanheimo–Stiefel transformation 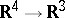 used in the regularization of the Kepler problem [a9] and associated to the Hopf fibration
used in the regularization of the Kepler problem [a9] and associated to the Hopf fibration 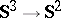 of fibre
of fibre 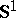 [a10]. The case
[a10]. The case 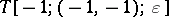 , where
, where 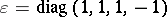 , corresponds to the Fock (stereographic) projection
, corresponds to the Fock (stereographic) projection 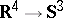 used in the quantum mechanical problem of the hydrogen atom [a11]. More generally, Hurwitz transformations are useful in number theory and in theoretical physics (classical and quantum mechanics, quantum field theory, local gauge symmetries). In particular, they can be useful for transforming a dynamical system in
used in the quantum mechanical problem of the hydrogen atom [a11]. More generally, Hurwitz transformations are useful in number theory and in theoretical physics (classical and quantum mechanics, quantum field theory, local gauge symmetries). In particular, they can be useful for transforming a dynamical system in 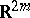 into a dynamical system in
into a dynamical system in 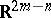 subject to
subject to  constraints. (Under such a transformation, the coupling constant of one system is exchanged with the energy of the other.)
constraints. (Under such a transformation, the coupling constant of one system is exchanged with the energy of the other.)
References
| [a1] | L.E. Dickson, "On quaternions and their generalization and the history of the eight square theorem" Ann. of Math. , 20 (1919) pp. 155 |
| [a2] | G.P. Wene, "A construction relating Clifford algebras and Cayley–Dickson algebras" J. Math. Phys. , 25 (1984) pp. 2351 |
| [a3] | D. Lambert, M. Kibler, "An algebraic and geometric approach to non-bijective quadratic transformations" J. Phys. A: Math. Gen. , 21 (1988) pp. 307 |
| [a4] | M. Kibler, P. Labastie, "Transformations generalizing the Levi-Civita, Kustaanheimo–Stiefel and Fock transformations" Y. Saint-Aubin (ed.) L. Vinet (ed.) , Group Theoretical Methods in Physics , World Sci. (1989) |
| [a5] | A. Hurwitz, "Über die Komposition der quadratischen Formen von beliebig vielen Variablen" Nachr. K. Gesellschaft Wissenschaft. Göttingen (1898) pp. 309 |
| [a6] | I.V. Polubarinov, "On the application of Hopf fiber bundles in quantum theory" , Report E2-84-607 , JINR: Dubna (Russia) (1984) |
| [a7] | M. Kibler, P. Winternitz, "Lie algebras under constraints and non-bijective transformations" J. Phys. A: Math. Gen. , 21 (1988) pp. 1787 |
| [a8] | T. Levi-Civita, "Sur la régularisation du problème des trois corps" Acta Math. , 42 (1918) pp. 99 |
| [a9] | P. Kustaanheimo, E. Stiefel, "Perturbation theory of Kepler motion based on spinor regularization" J. Reine Angew. Math. , 218 (1965) pp. 204 |
| [a10] | H. Hopf, "Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche" Math. Ann. , 104 (1931) pp. 637 |
| [a11] | V. Fock, "Zur Theorie des Wasserstoffatoms" Z. Phys. , 98 (1935) pp. 145 |
Hurwitz transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hurwitz_transformation&oldid=47281