Hotelling-T^2-distribution
The continuous probability distribution, concentrated on the positive semi-axis 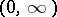 , with density
, with density
 |
depending on two integer parameters  (the number of degrees of freedom) and
(the number of degrees of freedom) and 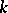 ,
, 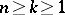 . For
. For 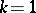 the Hotelling
the Hotelling 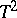 -distribution reduces to the Student distribution, and for any
-distribution reduces to the Student distribution, and for any 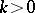 it can be regarded as a multivariate generalization of the Student distribution in the following sense. If a
it can be regarded as a multivariate generalization of the Student distribution in the following sense. If a 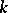 -dimensional random vector
-dimensional random vector 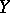 has the normal distribution with null vector of means and covariance matrix
has the normal distribution with null vector of means and covariance matrix 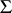 and if
and if
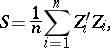 |
where the random vectors 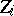 are independent, distributed as
are independent, distributed as 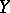 and also independent of
and also independent of 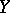 , then the random variable
, then the random variable 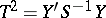 has the Hotelling
has the Hotelling 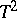 -distribution with
-distribution with  degrees of freedom (
degrees of freedom (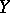 is a column vector and
is a column vector and 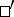 means transposition). If
means transposition). If 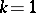 , then
, then
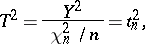 |
where the random variable 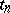 has the Student distribution with
has the Student distribution with  degrees of freedom. If in the definition of the random variable
degrees of freedom. If in the definition of the random variable 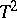 it is assumed that
it is assumed that 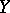 has the normal distribution with parameters
has the normal distribution with parameters 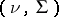 and
and  has the normal distribution with parameters
has the normal distribution with parameters 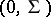 , then the corresponding distribution is called a non-central Hotelling
, then the corresponding distribution is called a non-central Hotelling 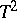 -distribution with
-distribution with  degrees of freedom and non-centrality parameter
degrees of freedom and non-centrality parameter  .
.
Hotelling's 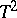 -distribution is used in mathematical statistics in the same situation as Student's
-distribution is used in mathematical statistics in the same situation as Student's 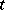 -distribution, but then in the multivariate case (see Multi-dimensional statistical analysis). If the results of observations
-distribution, but then in the multivariate case (see Multi-dimensional statistical analysis). If the results of observations 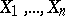 are independent normally-distributed random vectors with mean vector
are independent normally-distributed random vectors with mean vector  and non-degenerate covariance matrix
and non-degenerate covariance matrix 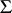 , then the statistic
, then the statistic
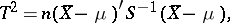 |
where
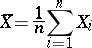 |
and
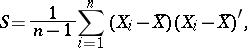 |
has the Hotelling 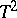 -distribution with
-distribution with 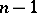 degrees of freedom. This fact forms the basis of the Hotelling test. For numerical calculations one uses tables of the beta-distribution or of the Fisher
degrees of freedom. This fact forms the basis of the Hotelling test. For numerical calculations one uses tables of the beta-distribution or of the Fisher 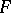 -distribution, because the random variable
-distribution, because the random variable 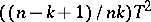 has the
has the 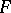 -distribution with
-distribution with 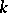 and
and 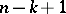 degrees of freedom.
degrees of freedom.
The Hotelling 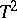 -distribution was proposed by H. Hotelling [1] for testing equality of means of two normal populations.
-distribution was proposed by H. Hotelling [1] for testing equality of means of two normal populations.
References
| [1] | H. Hotelling, "The generalization of Student's ratio" Ann. Math. Stat. , 2 (1931) pp. 360–378 |
| [2] | T.W. Anderson, "An introduction to multivariate statistical analysis" , Wiley (1984) |
Hotelling-T^2-distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hotelling-T%5E2-distribution&oldid=47274