Horocycle flow

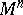A flow in the space of bihedra of an -dimensional Riemannian manifold (usually closed) for which the concept of a horocycle is defined; the horocycle flow describes the movement of the bihedra along the horocycles which they define.

The basic cases in which the concept of a horocycle is defined are those in which the curvature of the Riemannian metric is negative, and either 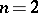or the curve is constant. With a bihedron, i.e. an orthonormal -frame 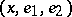(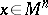; are mutually orthogonal unit tangent vectors at the point ) is associated the horocycle 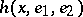through in the direction of 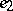. It is situated on the horosphere 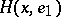through , the 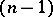-dimensional manifold orthogonal to the family of geodesic lines, asymptotic (in the positive direction) to the geodesic line which passes through in the direction of 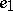. The direction on 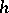defined by is taken to be positive (in case 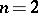this is the only role of 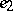; 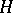and can have self-intersections; the simplest way to avoid the ambiguity which can arise from this is to carry out analogous constructions not in 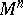, but in its universal covering manifold — when the curvature is constant, this is the ordinary -dimensional Lobachevskii space — and to project the horocycle obtained there into 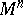). Under the action of a horocycle flow, the bihedron 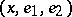during time 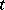passes to

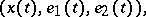where 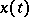, when 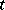increases, moves at unit velocity along 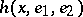in the positive direction, the unit vector 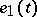is orthogonal to 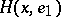at the point 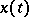(the choice of one of the two possible directions for 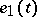is made by continuity) and .

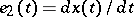Horocycle flows were studied because they played an important role in the research of geodesic flows (cf. Geodesic flow) on manifolds of negative curvature [1]. Now this role is played by certain foliations (cf. Foliation) arising from the theory of 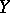-systems (cf. 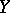-system), and horocycle flows became a research subject in its own right. The properties of a horocycle flow have been well established (see [2]–[7], [11]). For various generalizations, see –[10].

References

[1]	E. Hopf, "Statistik des geodätischen Linien in Manningfaltigkeiten negativer Krümmung" Ber. Verh. Sächs. Akad. Wiss. Leipzig , 91 (1939) pp. 261–304
[2]	O.S. Parasyuk, "Horocycle flows on surfaces of constant negative curvature" Uspekhi Mat. Nauk. , 8 : 3 (1953) pp. 125–126 (In Russian)
[3]	B.M. Gurevich, "The entropy of horocycle flows" Soviet Math. Dokl. , 2 (1961) pp. 124–126 Dokl. Akad. Nauk. SSSR , 136 : 4 (1961) pp. 768–770
[4]	H. Furstenberg, "The unique ergodicity of the horocycle flow" A. Beck (ed.) , Recent advances in topological dynamics , Lect. notes in math. , 318 , Springer (1973) pp. 95–115
[5]	B. Marcus, "Unique ergodicity of the horocycle flow: variable negative curvature case" Israel J. Math. , 21 : 2–3 (1975) pp. 133–144
[6]	B. Marcus, "Ergodic properties of horocycle flows for surfaces of negative curvature" Ann. of Math. , 105 : 1 (1977) pp. 81–105
[7]	B. Marcus, "The horocycle flow is mixing of all degrees" Invent. Math. , 46 : 3 (1978) pp. 201–209
[8a]	L.W. Green, "The generalized geodesic flow" Duke Math. J. , 41 : 1 (1974) pp. 115–126
[8b]	L.W. Green, "Correction on: The generalized geodesic flow" Duke. Math. J. , 42 (1975) pp. 381
[9]	R. Bowen, "Weak mixing and unique ergodicity on homogeneous spaces" Israel J. Math. , 23 : 3–4 (1976) pp. 267–273
[10]	R. Bowen, B. Marcus, "Unique ergodicity for horocycle foliations" Israel J. Math. , 26 : 1 (1977) pp. 43–67
[11]	M. Ratner, "Rigidity of horocycle flows" Ann. of Math. , 115 : 3 (1982) pp. 597–614