Difference between revisions of "Horocycle flow"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Hopf, "Statistik des geodätischen Linien in Manningfaltigkeiten negativer Krümmung" ''Ber. Verh. Sächs. Akad. Wiss. Leipzig'' , '''91''' (1939) pp. 261–304</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> O.S. Parasyuk, "Horocycle flows on surfaces of constant negative curvature" ''Uspekhi Mat. Nauk.'' , '''8''' : 3 (1953) pp. 125–126 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.M. Gurevich, "The entropy of horocycle flows" ''Soviet Math. Dokl.'' , '''2''' (1961) pp. 124–126 ''Dokl. Akad. Nauk. SSSR'' , '''136''' : 4 (1961) pp. 768–770</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Furstenberg, "The unique ergodicity of the horocycle flow" A. Beck (ed.) , ''Recent advances in topological dynamics'' , ''Lect. notes in math.'' , '''318''' , Springer (1973) pp. 95–115 {{MR|0393339}} {{ZBL|0256.58009}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Marcus, "Unique ergodicity of the horocycle flow: variable negative curvature case" ''Israel J. Math.'' , '''21''' : 2–3 (1975) pp. 133–144 {{MR|0407902}} {{ZBL|0314.58013}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Marcus, "Ergodic properties of horocycle flows for surfaces of negative curvature" ''Ann. of Math.'' , '''105''' : 1 (1977) pp. 81–105 {{MR|0458496}} {{ZBL|}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B. Marcus, "The horocycle flow is mixing of all degrees" ''Invent. Math.'' , '''46''' : 3 (1978) pp. 201–209 {{MR|0488168}} {{ZBL|0395.28012}} </TD></TR><TR><TD valign="top">[8a]</TD> <TD valign="top"> L.W. Green, "The generalized geodesic flow" ''Duke Math. J.'' , '''41''' : 1 (1974) pp. 115–126 {{MR|0370659}} {{ZBL|0283.58011}} {{ZBL|0935.53037}} </TD></TR><TR><TD valign="top">[8b]</TD> <TD valign="top"> L.W. Green, "Correction on: The generalized geodesic flow" ''Duke. Math. J.'' , '''42''' (1975) pp. 381</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> R. Bowen, "Weak mixing and unique ergodicity on homogeneous spaces" ''Israel J. Math.'' , '''23''' : 3–4 (1976) pp. 267–273 {{MR|0407233}} {{ZBL|0338.43014}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> R. Bowen, B. Marcus, "Unique ergodicity for horocycle foliations" ''Israel J. Math.'' , '''26''' : 1 (1977) pp. 43–67 {{MR|0451307}} {{ZBL|0346.58009}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> M. Ratner, "Rigidity of horocycle flows" ''Ann. of Math.'' , '''115''' : 3 (1982) pp. 597–614 {{MR|0657240}} {{ZBL|0506.58030}} </TD></TR></table> |
Revision as of 16:58, 15 April 2012
A flow in the space of bihedra of an  -dimensional Riemannian manifold
-dimensional Riemannian manifold 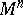 (usually closed) for which the concept of a horocycle is defined; the horocycle flow describes the movement of the bihedra along the horocycles which they define.
(usually closed) for which the concept of a horocycle is defined; the horocycle flow describes the movement of the bihedra along the horocycles which they define.
The basic cases in which the concept of a horocycle is defined are those in which the curvature of the Riemannian metric is negative, and either 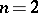 or the curve is constant. With a bihedron, i.e. an orthonormal
or the curve is constant. With a bihedron, i.e. an orthonormal  -frame
-frame 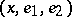 (
(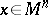 ;
;  are mutually orthogonal unit tangent vectors at the point
are mutually orthogonal unit tangent vectors at the point  ) is associated the horocycle
) is associated the horocycle 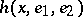 through
through  in the direction of
in the direction of 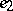 . It is situated on the horosphere
. It is situated on the horosphere 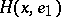 through
through  , the
, the 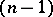 -dimensional manifold orthogonal to the family of geodesic lines, asymptotic (in the positive direction) to the geodesic line which passes through
-dimensional manifold orthogonal to the family of geodesic lines, asymptotic (in the positive direction) to the geodesic line which passes through  in the direction of
in the direction of 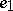 . The direction on
. The direction on 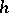 defined by
defined by  is taken to be positive (in case
is taken to be positive (in case 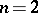 this is the only role of
this is the only role of 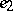 ;
; 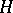 and
and  can have self-intersections; the simplest way to avoid the ambiguity which can arise from this is to carry out analogous constructions not in
can have self-intersections; the simplest way to avoid the ambiguity which can arise from this is to carry out analogous constructions not in 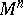 , but in its universal covering manifold — when the curvature is constant, this is the ordinary
, but in its universal covering manifold — when the curvature is constant, this is the ordinary  -dimensional Lobachevskii space — and to project the horocycle obtained there into
-dimensional Lobachevskii space — and to project the horocycle obtained there into 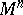 ). Under the action of a horocycle flow, the bihedron
). Under the action of a horocycle flow, the bihedron 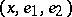 during time
during time 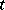 passes to
passes to
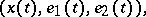 |
where 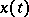 , when
, when 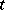 increases, moves at unit velocity along
increases, moves at unit velocity along 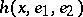 in the positive direction, the unit vector
in the positive direction, the unit vector 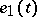 is orthogonal to
is orthogonal to 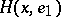 at the point
at the point 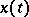 (the choice of one of the two possible directions for
(the choice of one of the two possible directions for 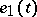 is made by continuity) and
is made by continuity) and 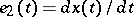 .
.
Horocycle flows were studied because they played an important role in the research of geodesic flows (cf. Geodesic flow) on manifolds of negative curvature [1]. Now this role is played by certain foliations (cf. Foliation) arising from the theory of 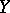 -systems (cf.
-systems (cf. 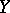 -system), and horocycle flows became a research subject in its own right. The properties of a horocycle flow have been well established (see [2]–[7], [11]). For various generalizations, see –[10].
-system), and horocycle flows became a research subject in its own right. The properties of a horocycle flow have been well established (see [2]–[7], [11]). For various generalizations, see –[10].
References
| [1] | E. Hopf, "Statistik des geodätischen Linien in Manningfaltigkeiten negativer Krümmung" Ber. Verh. Sächs. Akad. Wiss. Leipzig , 91 (1939) pp. 261–304 |
| [2] | O.S. Parasyuk, "Horocycle flows on surfaces of constant negative curvature" Uspekhi Mat. Nauk. , 8 : 3 (1953) pp. 125–126 (In Russian) |
| [3] | B.M. Gurevich, "The entropy of horocycle flows" Soviet Math. Dokl. , 2 (1961) pp. 124–126 Dokl. Akad. Nauk. SSSR , 136 : 4 (1961) pp. 768–770 |
| [4] | H. Furstenberg, "The unique ergodicity of the horocycle flow" A. Beck (ed.) , Recent advances in topological dynamics , Lect. notes in math. , 318 , Springer (1973) pp. 95–115 MR0393339 Zbl 0256.58009 |
| [5] | B. Marcus, "Unique ergodicity of the horocycle flow: variable negative curvature case" Israel J. Math. , 21 : 2–3 (1975) pp. 133–144 MR0407902 Zbl 0314.58013 |
| [6] | B. Marcus, "Ergodic properties of horocycle flows for surfaces of negative curvature" Ann. of Math. , 105 : 1 (1977) pp. 81–105 MR0458496 |
| [7] | B. Marcus, "The horocycle flow is mixing of all degrees" Invent. Math. , 46 : 3 (1978) pp. 201–209 MR0488168 Zbl 0395.28012 |
| [8a] | L.W. Green, "The generalized geodesic flow" Duke Math. J. , 41 : 1 (1974) pp. 115–126 MR0370659 Zbl 0283.58011 Zbl 0935.53037 |
| [8b] | L.W. Green, "Correction on: The generalized geodesic flow" Duke. Math. J. , 42 (1975) pp. 381 |
| [9] | R. Bowen, "Weak mixing and unique ergodicity on homogeneous spaces" Israel J. Math. , 23 : 3–4 (1976) pp. 267–273 MR0407233 Zbl 0338.43014 |
| [10] | R. Bowen, B. Marcus, "Unique ergodicity for horocycle foliations" Israel J. Math. , 26 : 1 (1977) pp. 43–67 MR0451307 Zbl 0346.58009 |
| [11] | M. Ratner, "Rigidity of horocycle flows" Ann. of Math. , 115 : 3 (1982) pp. 597–614 MR0657240 Zbl 0506.58030 |
Horocycle flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Horocycle_flow&oldid=15745