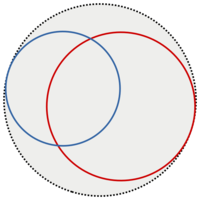
Horocycle
oricycle, limiting line
The orthogonal trajectory of parallel lines in the Lobachevskii plane in a certain direction. A horocycle can be considered as a circle with centre at infinity. Horocycles generated by one pencil of parallel lines are congruent, concentric (i.e. cut out congruent segments on the lines of the pencil), non-closed, and concave to the side of parallelism of the lines of the pencil. The curvature of a horocycle is constant. In Poincaré's model, a horocycle is a circle touching the absolute from within.
A straight line and a horocycle either do not have common points, touch each other, intersect at two points at the same angle, or intersect at one point at a right angle.
Two, and only two, horocycles pass through two points of the Lobachevskii plane.
References
| [1] | V.F. Kagan, "Foundations of geometry" , 1–2 , Moscow-Leningrad (1949–1956) (In Russian) |
| [2] | A.P. Norden, "Elementare Einführung in die Lobatschewskische Geometrie" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
| [3] | N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) Zbl 0108.16203 |
| [a1] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) |
Horocycle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Horocycle&oldid=54010