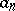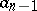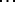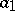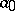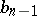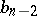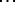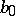Horner scheme
A method for obtaining the incomplete fraction and the remainder in the division of a polynomial
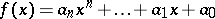 | (1) |
by a binomial  , where all the coefficients
, where all the coefficients  lie in a certain field, e.g. in the field of complex numbers. Any polynomial
lie in a certain field, e.g. in the field of complex numbers. Any polynomial  can be uniquely represented in the form
can be uniquely represented in the form
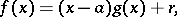 |
where  is the incomplete fraction, while
is the incomplete fraction, while  is the remainder which, according to the Bezout theorem, equals
is the remainder which, according to the Bezout theorem, equals  . The coefficients of
. The coefficients of  and
and  are calculated by the recurrence formulas
are calculated by the recurrence formulas
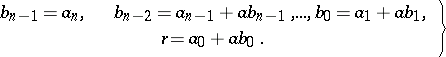 | (2) |
The following table:'
<tbody> </tbody>
|
whose upper line is given, while the lower line is filled in accordance with the formulas (2), is used in the computations. In fact, this method is identical with the method of Ch'in Chiu-Shao employed in medieval China. At the beginning of the 19th century it was rediscovered, almost simultaneously, by W.G. Horner [1] and P. Ruffini [1].
References
| [1] | W.G. Horner, Philos. Transact. Roy. Soc. London Ser. A , 1 (1819) pp. 308–335 |
| [2] | P. Ruffini, Mem. Coronata Soc. Ital. Sci. , 9 (1802) pp. 44–526 |
Comments
Horner's scheme is used for the efficient evaluation of polynomials. The straightforward evaluation of  for a given value
for a given value  by computing the powers
by computing the powers  and forming the linear combination according to (1) would require
and forming the linear combination according to (1) would require  multiplications. However, by writing
multiplications. However, by writing  in the "nested" form
in the "nested" form
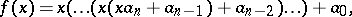 |
only  (sequential) multiplications are involved. It is easily verified that using this nested representation the work consists of the computation steps given by (2). Since
(sequential) multiplications are involved. It is easily verified that using this nested representation the work consists of the computation steps given by (2). Since 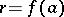 , the evaluation of
, the evaluation of  requires
requires  instead of
instead of  multiplications.
multiplications.
References
| [a1] | F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1974) |
| [a2] | F. Cajori, "A history of mathematics" , Chelsea, reprint (1980) |
Horner scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Horner_scheme&oldid=18660