An operation defined on the groups 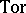 and
and  . One considers
. One considers 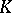 -algebras
-algebras  and
and  over a commutative ring
over a commutative ring  . The derived functors (cf. Derived functor)
. The derived functors (cf. Derived functor)  and
and  over them may be combined with one another by means of four homomorphisms, known as homology products:
over them may be combined with one another by means of four homomorphisms, known as homology products:
Here, 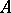 and
and 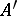 are right or left
are right or left 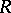 -modules,
-modules, 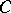 and
and 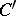 are right or left
are right or left  -modules, while the symbol
-modules, while the symbol 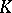 is omitted in all functors. The last two homomorphisms are defined only if the algebras
is omitted in all functors. The last two homomorphisms are defined only if the algebras  and
and 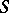 are projective over
are projective over 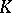 and if
and if 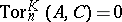 for all
for all 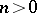 . If certain supplementary restrictions are made, intrinsic products can be obtained which connect
. If certain supplementary restrictions are made, intrinsic products can be obtained which connect 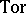 and
and  over the same ring.
over the same ring.
All four products can be obtained from formulas representing the functors 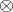 and
and  by replacing the arguments by the corresponding resolutions [1]. The multiplication
by replacing the arguments by the corresponding resolutions [1]. The multiplication  permits the following interpretation in terms of Yoneda products. Let
permits the following interpretation in terms of Yoneda products. Let
be exact sequences of 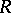 - and
- and 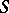 -modules, respectively, that are representatives of the corresponding equivalence classes in
-modules, respectively, that are representatives of the corresponding equivalence classes in 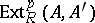 and
and  . Multiplying the former tensorially from the right by
. Multiplying the former tensorially from the right by  and the latter from the left by
and the latter from the left by 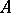 , one obtains exact sequences
, one obtains exact sequences
which can be combined into the exact sequence
This sequence can be regarded as the representative of an equivalence class in the group
The product 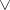 in the cohomology space
in the cohomology space 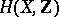 of a topological space
of a topological space 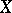 with coefficients in the ring of integers
with coefficients in the ring of integers 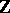 is known as the Alexander–Kolmogorov product or the
is known as the Alexander–Kolmogorov product or the 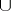 -product.
-product.
References
| [1] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [2] | S. MacLane, "Homology" , Springer (1963) |
How to Cite This Entry:
Homology product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homology_product&oldid=18757
This article was adapted from an original article by V.E. Govorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article and
and  . One considers
. One considers 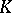 -algebras
-algebras  and
and  over a commutative ring
over a commutative ring  . The derived functors (cf. Derived functor)
. The derived functors (cf. Derived functor)  and
and  over them may be combined with one another by means of four homomorphisms, known as homology products:
over them may be combined with one another by means of four homomorphisms, known as homology products:
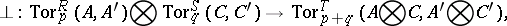
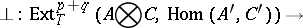
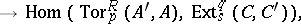
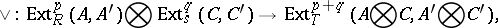
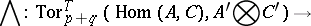
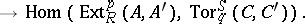
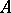 and
and 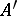 are right or left
are right or left 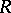 -modules,
-modules, 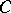 and
and 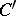 are right or left
are right or left  -modules, while the symbol
-modules, while the symbol 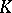 is omitted in all functors. The last two homomorphisms are defined only if the algebras
is omitted in all functors. The last two homomorphisms are defined only if the algebras  and
and 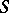 are projective over
are projective over 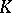 and if
and if 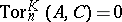 for all
for all 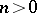 . If certain supplementary restrictions are made, intrinsic products can be obtained which connect
. If certain supplementary restrictions are made, intrinsic products can be obtained which connect  and
and  over the same ring.
over the same ring.
 and
and  by replacing the arguments by the corresponding resolutions [1]. The multiplication
by replacing the arguments by the corresponding resolutions [1]. The multiplication  permits the following interpretation in terms of Yoneda products. Let
permits the following interpretation in terms of Yoneda products. Let
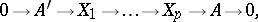
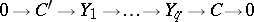
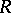 - and
- and 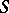 -modules, respectively, that are representatives of the corresponding equivalence classes in
-modules, respectively, that are representatives of the corresponding equivalence classes in 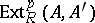 and
and  . Multiplying the former tensorially from the right by
. Multiplying the former tensorially from the right by  and the latter from the left by
and the latter from the left by 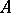 , one obtains exact sequences
, one obtains exact sequences
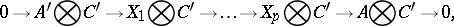
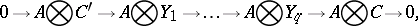
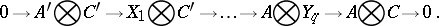
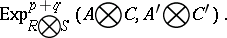
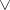 in the cohomology space
in the cohomology space 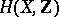 of a topological space
of a topological space 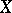 with coefficients in the ring of integers
with coefficients in the ring of integers 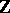 is known as the Alexander–Kolmogorov product or the
is known as the Alexander–Kolmogorov product or the 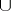 -product.
-product.