Homological perturbation theory
A theory concerning itself with a collection of techniques for deriving chain complexes which are both smaller and chain homotopy equivalent to a given chain complex (cf. also Complex (in homological algebra)). It is motivated by the desire to find effective algorithms in homological algebra. The cornerstone of the theory is an important algorithm which, when convergent, is commonly called the "perturbation lemma" . To understand the statement of the perturbation lemma, some preliminary notation is needed.
Strong deformation retraction data.
It will be assumed that 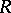 is a commutative ring with unit and that all chain complexes are over
is a commutative ring with unit and that all chain complexes are over 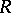 and free (cf. also Simplicial complex). A strong deformation retract from
and free (cf. also Simplicial complex). A strong deformation retract from 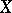 to
to 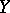 consists of two chain complexes
consists of two chain complexes 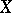 and
and 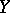 such that there are chain mappings
such that there are chain mappings 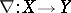 ,
,  , and a chain homotopy
, and a chain homotopy 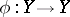 such that
such that 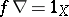 (the identity mapping on
(the identity mapping on  ) and
) and 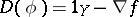 (cf. also Complex (in homological algebra)). Here it is assumed that the differentials
(cf. also Complex (in homological algebra)). Here it is assumed that the differentials 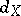 and
and 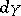 of
of 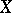 and
and 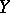 , respectively, are of degree
, respectively, are of degree 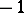 , the degree of
, the degree of 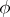 is
is 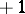 and
and 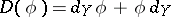 , i.e.
, i.e. 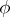 is a chain homotopy between the identity and
is a chain homotopy between the identity and 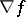 , while
, while 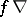 is the identity. A standard notation for an strong deformation retract is the following:
is the identity. A standard notation for an strong deformation retract is the following:
 | (a1) |
The notion of a strong deformation retract is essentially equivalent to what is called a contraction in [a5].
Side conditions.
There are three additional conditions for a strong deformation retract which are needed to achieve both theoretical and computational results. They are called the side conditions: 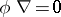 ,
, 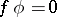 , and
, and 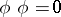 . Fortunately, these may always be satisfied as follows: if the first two conditions do not hold, replace
. Fortunately, these may always be satisfied as follows: if the first two conditions do not hold, replace  by
by 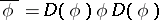 , then the new data given by
, then the new data given by  ,
, 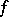 , and
, and 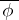 defines a strong deformation retract in which the first two conditions hold. If the third condition does not hold, and the first two do, replace
defines a strong deformation retract in which the first two conditions hold. If the third condition does not hold, and the first two do, replace 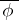 by
by 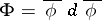 and the new data given by
and the new data given by  ,
,  , and
, and 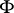 defines a strong deformation retract in which all conditions hold [a17].
defines a strong deformation retract in which all conditions hold [a17].
Transference problem.
A transference problem consists of a strong deformation retract (a1) together with another differential 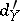 on
on 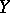 . The difference
. The difference  is called the initiator. The problem is to determine changes
is called the initiator. The problem is to determine changes  ,
, 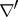 ,
, 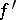 , and
, and 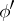 such that
such that
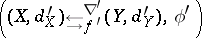 |
is a strong deformation retract. A useful variation of the transference problem, equivalent to it, is stated in terms of splitting homotopies. A splitting homotopy for a complex 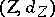 is a degree-
is a degree-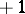 mapping
mapping 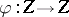 such that
such that 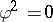 and
and 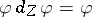 . It is not difficult to see that complexes
. It is not difficult to see that complexes 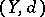 with a splitting homotopy
with a splitting homotopy  are in bijective correspondence (up to chain equivalence) with strong deformation retracts (a1). The correspondence is given by noting that if one has a strong deformation retract,
are in bijective correspondence (up to chain equivalence) with strong deformation retracts (a1). The correspondence is given by noting that if one has a strong deformation retract, 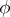 is indeed a splitting homotopy. Conversely, given a splitting homotopy
is indeed a splitting homotopy. Conversely, given a splitting homotopy 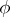 , if
, if 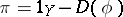 , then one has
, then one has 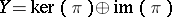 and setting,
and setting,  , a strong deformation retract results by taking
, a strong deformation retract results by taking 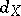 to be the restriction of
to be the restriction of 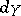 to
to 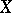 ,
,  to be the inclusion mapping, and
to be the inclusion mapping, and 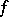 to be the projection. The transference problem in these terms is as follows.
to be the projection. The transference problem in these terms is as follows.
Given a splitting homotopy 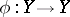 , and a new differential
, and a new differential 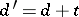 on
on 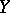 , find a new splitting homotopy
, find a new splitting homotopy 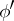 on
on 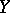 (relative to
(relative to 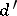 ) such that, as
) such that, as 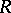 -modules,
-modules, 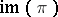 is isomorphic to
is isomorphic to 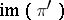 (where
(where 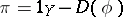 and
and 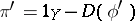 ). See [a1] for full details.
). See [a1] for full details.
Solution to the transference problem.
The perturbation lemma gives conditions under which the transference problem can be solved. In terms of splitting homotopies, it can be stated quite simply, as follows.
Suppose that 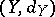 is a chain complex and
is a chain complex and  is a splitting homotopy. If
is a splitting homotopy. If 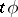 is nilpotent in each homogeneous degree
is nilpotent in each homogeneous degree 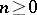 , then
, then
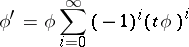 | (a2) |
(which is well-defined since 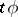 is nilpotent in each degree) is a splitting homotopy which solves the transference problem. Furthermore, under mild assumptions, any solution to the transference is conjugate to this solution by a chain homotopy equivalence [a1].
is nilpotent in each degree) is a splitting homotopy which solves the transference problem. Furthermore, under mild assumptions, any solution to the transference is conjugate to this solution by a chain homotopy equivalence [a1].
Originally, this was stated in terms of strong deformation retracts [a2], [a6] (although the uniqueness result first appears in [a1]). These early works were influenced by [a19]. For that setting, let 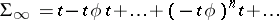 . It is easy to see that in terms of strong deformation retracts, if the hypotheses of the perturbation lemma hold, the mappings
. It is easy to see that in terms of strong deformation retracts, if the hypotheses of the perturbation lemma hold, the mappings 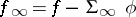 ,
, 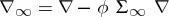 ,
, 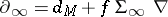 , and
, and 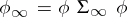 solve the transference problem, using the fact that
solve the transference problem, using the fact that 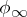 is exactly
is exactly  from above along with the correspondence between strong deformation retracts and splitting homotopies.
from above along with the correspondence between strong deformation retracts and splitting homotopies.
The formula (a2) and the uniqueness result have far-reaching consequences in homological algebra and topology. Many seemingly unrelated results may be consolidated by these methods and it can also be used to find new results. The main technique is to set up a transference problem and prove convergence of (a2).
Applications.
An application is given in [a2] to explain the Hirsch complex, and in [a6] to obtain twisted tensor product complexes in the sense of [a3] for (simplicial) fibrations. The application in [a6] was generalized to iterated fibrations in [a11] and these applications were further generalized to obtain much smaller complexes for iterated fibrations in [a17].
Applications to the derivation of "small" resolutions over group rings of nilpotent groups and certain solvable groups and monoids are given in [a14]. Applications to resolutions over certain filtered algebras are given in [a15], as well as the observation that the perturbation lemma gives rise to an exact formula for all the differentials in a wide class of spectral sequences (involving filtered algebras). Computer algebra has been used to obtain concrete calculations using these results [a16], [a14]. To give a quick and rough idea of how this can be done, think of a given filtered augmented algebra  such that, as
such that, as 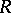 -modules, the associated graded object
-modules, the associated graded object 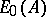 is isomorphic to
is isomorphic to 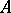 (e.g.
(e.g. 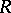 is a field) and one has a resolution of the form
is a field) and one has a resolution of the form 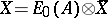 of
of 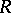 over
over 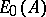 with the property that
with the property that 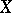 is a strong deformation retract of the bar-construction resolution
is a strong deformation retract of the bar-construction resolution 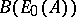 [a20] (cf. also Standard construction). Since as
[a20] (cf. also Standard construction). Since as 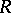 -modules,
-modules, 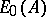 is isomorphic to
is isomorphic to 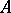 , one can see two differentials on the underlying
, one can see two differentials on the underlying 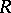 -module structure of
-module structure of 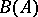 : The one coming from
: The one coming from 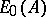 and the one coming from
and the one coming from 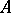 . Taking the initiator
. Taking the initiator 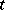 to be the difference of the two differentials, one has a transference problem. When the hypothesis of the perturbation lemma is satisfied, this gives a resolution of
to be the difference of the two differentials, one has a transference problem. When the hypothesis of the perturbation lemma is satisfied, this gives a resolution of 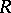 over
over 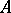 which is as small as the original one over
which is as small as the original one over 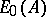 . The requirements for all of this are not at all uncommonly found to hold.
. The requirements for all of this are not at all uncommonly found to hold.
Applications to the derivation of (co-) 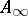 -structures were given in [a7], [a8], and in [a12]. These applications proceed by setting up a transference problem involving a strong deformation retract of
-structures were given in [a7], [a8], and in [a12]. These applications proceed by setting up a transference problem involving a strong deformation retract of 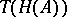 into
into 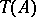 , where
, where  is a differential graded augmented algebra and
is a differential graded augmented algebra and  is the tensor module functor. The point is that the underlying module structure for both ordinary Tor and differential Tor [a4] is given by
is the tensor module functor. The point is that the underlying module structure for both ordinary Tor and differential Tor [a4] is given by 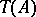 , the only difference being the differentials. Taking the difference of these differentials to be the initiator, and showing that (a2) converges in this case, one obtains a differential
, the only difference being the differentials. Taking the difference of these differentials to be the initiator, and showing that (a2) converges in this case, one obtains a differential  on
on 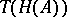 and a strong deformation retract of this new complex into the differential Tor bar-construction
and a strong deformation retract of this new complex into the differential Tor bar-construction  . In this case it was shown in [a8], and independently in [a12], that
. In this case it was shown in [a8], and independently in [a12], that  is actually a co-derivation (the proof of this fact is non-trivial). Thus, the perturbation lemma gives, in this case, an algorithm for deriving an
is actually a co-derivation (the proof of this fact is non-trivial). Thus, the perturbation lemma gives, in this case, an algorithm for deriving an 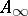 -structure on
-structure on 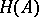 which is equivalent to
which is equivalent to 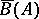 . This application has come to be known as the tensor trick. Applications to the homology of loop spaces can be obtained by these methods [a9], [a12].
. This application has come to be known as the tensor trick. Applications to the homology of loop spaces can be obtained by these methods [a9], [a12].
Generalized Gugenheim–Munkholm construction.
As hinted at above, homological perturbation theory also involves the consolidation of sometimes apparently unrelated techniques and results. For example, in [a10] it was shown that if one has a strong deformation retract (a1) where both  and
and  are differential graded augmented algebras and the mapping
are differential graded augmented algebras and the mapping  is an algebra mapping, any twisting cochain [a10]
is an algebra mapping, any twisting cochain [a10] 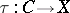 for a differential co-algebra
for a differential co-algebra 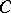 can be lifted to
can be lifted to 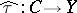 (with
(with 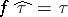 ). V.K.A.M. Gugenheim and H.J. Munkholm give an inductive formula:
). V.K.A.M. Gugenheim and H.J. Munkholm give an inductive formula:
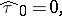 |
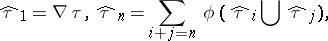 |
where 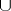 is the convolution product for mappings
is the convolution product for mappings 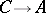 (
(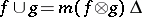 , where
, where 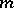 is the product in
is the product in 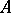 and
and 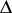 is the co-product in
is the co-product in 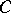 ). The mapping
). The mapping 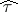 is
is 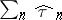 (conditions for convergence are given in [a10]).
(conditions for convergence are given in [a10]).
Staying in the special setting of [a10], and furthermore assuming that 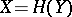 is the homology of the differential graded augmented algebra
is the homology of the differential graded augmented algebra 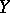 , puts one in the (general) formal setting (see [a18] for the characteristic zero case). In this case, the universal twisting cochain
, puts one in the (general) formal setting (see [a18] for the characteristic zero case). In this case, the universal twisting cochain 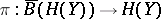 lifts to a twisting cochain
lifts to a twisting cochain 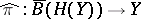 . It was shown in [a7] that, in this case, not only does the
. It was shown in [a7] that, in this case, not only does the 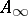 -structure on
-structure on 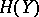 collapse to the bar-construction (as it must by formality), but the induced mapping
collapse to the bar-construction (as it must by formality), but the induced mapping 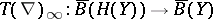 followed by the universal twisting cochain
followed by the universal twisting cochain 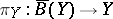 , is exactly the mapping
, is exactly the mapping  above.
above.
The construction given in [a10] can be applied in a purely combinatorial way for any strong deformation retract (a1) for any degree-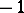 mapping
mapping 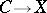 . Of course, one cannot even talk about twisting cochains in this context since
. Of course, one cannot even talk about twisting cochains in this context since  might not be an algebra (much less
might not be an algebra (much less  be an algebra mapping). Nevertheless, if this construction is applied to the case when
be an algebra mapping). Nevertheless, if this construction is applied to the case when 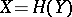 and
and 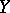 is an algebra (no extra assumptions on
is an algebra (no extra assumptions on 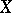 or
or 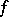 ) and
) and  is the module mapping defined combinatorially in exactly the same way as the universal twisting cochain, then the result of [a7] generalizes to this case, i.e. the composite of the mapping
is the module mapping defined combinatorially in exactly the same way as the universal twisting cochain, then the result of [a7] generalizes to this case, i.e. the composite of the mapping  followed by the universal twisting cochain is exactly the mapping
followed by the universal twisting cochain is exactly the mapping 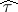 . But in fact, more is known. By a small alteration of the construction, one can actually obtain the
. But in fact, more is known. By a small alteration of the construction, one can actually obtain the 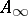 -structure as well:
-structure as well:
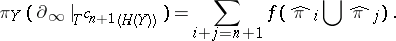 |
Thus, the 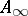 -structure of the tensor trick is completely determined by the generalized construction
-structure of the tensor trick is completely determined by the generalized construction 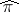 . The proof of this, which is not immediate, as well as additional results are given in [a13].
. The proof of this, which is not immediate, as well as additional results are given in [a13].
All of the references in the papers cited below should be perused for a more complete picture of the applications, but one should keep in mind that this is presently (1998) an active field and new results are constantly evolving.
References
| [a1] | D. Barnes, L. Lambe, "Fixed point approach to homological perturbation theory" Proc. Amer. Math. Soc. , 112 (1991) pp. 881–892 |
| [a2] | R. Brown, "The twisted Eilenberg–Zilber theorem" , Celebrazioni Archimedee del Secolo XX, Simposio di Topologia (1967) pp. 34–37 |
| [a3] | E.H. Brown, "Twisted tensor products" Ann. of Math. , 1 (1959) pp. 223–246 |
| [a4] | H. Cartan, "Algèbres d'Eilenberg–MacLane et homotopie" Sém. Henri Cartan (1954/5) |
| [a5] | S. Eilenberg, S. MacLane, "On the groups 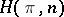 I" Ann. of Math. , 58 (1953) pp. 55–106 I" Ann. of Math. , 58 (1953) pp. 55–106 |
| [a6] | V.K.A.M. Gugenheim, "On the chain complex of a fibration" Illinois J. Math. , 3 (1972) pp. 398–414 |
| [a7] | V.K.A.M. Gugenheim, L. Lambe, "Perturbation theory in differential homological algebra I" Illinois J. Math. , 33 (1989) pp. 566–582 |
| [a8] | V.K.A.M. Gugenheim, L. Lambe, J. Stasheff, "Perturbation theory in differential homological algebra II" Illinois J. Math. , 35 (1991) pp. 359–373 |
| [a9] | V.K.A.M. Gugenheim, L. Lambe, J. Stasheff, "Algebraic aspects of Chen's iterated integrals" Illinois J. Math. , 34 (1990) pp. 485–502 |
| [a10] | V.K.A.M. Gugenheim, H.J. Munkholm, "On the extended functoriality of Tor and Cotor" J. Pure Appl. Algebra , 4 (1974) pp. 9–29 |
| [a11] | J. Hübschmann, "The homotopy type of 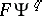 , the complex and symplectic cases" Contemp. Math. , 55 (1986) pp. 487–518 , the complex and symplectic cases" Contemp. Math. , 55 (1986) pp. 487–518 |
| [a12] | J. Hübschmann, T. Kadeishvili, "Small models for chain algebras" Math. Z. , 207 : 2 (1991) pp. 245–280 |
| [a13] | J. Johansson, L. Lambe, "Transferring algebra structures up to homology equivalence" Math. Scand. , 88 : 2 (2001) |
| [a14] | L. Lambe, "Resolutions that split off of the bar construction" J. Pure Appl. Algebra , 84 (1993) pp. 311–329 |
| [a15] | L. Lambe, "Homological perturbation theory, Hochschild homology and formal groups" Contemp. Math. , 134 (1992) |
| [a16] | L. Lambe, "Resolutions via homological perturbation" J. Symbolic Comp. , 12 (1991) pp. 71–87 |
| [a17] | L. Lambe, J. Stasheff, "Applications of perturbation theory to iterated fibrations" Manuscripta Math. , 58 (1987) pp. 363–376 |
| [a18] | D. Sullivan, "Infinitesimal computations in topology" Publ. Math. IHES , 47 (1977) pp. 269–331 |
| [a19] | W. Shih, "Homology des espaces fibrés" Publ. Math. IHES , 13 (1962) pp. 93–176 |
| [a20] | S. MacLane, "Homology" , Grundl. Math. Wissenschaft. , 114 , Springer (1967) |
Homological perturbation theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homological_perturbation_theory&oldid=14253