Holonomy group
A characteristic of a connection on a fibre bundle. The holonomy group is defined for a principal fibre bundle  with a Lie structure group
with a Lie structure group  and (second countable) base
and (second countable) base  on which an infinitesimal connection
on which an infinitesimal connection  is given. It is also defined for any fibre bundle
is given. It is also defined for any fibre bundle  associated to
associated to  whose fibres are copies of some representation space
whose fibres are copies of some representation space  of
of  .
.
The connection  on
on 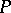 (or, respectively, on
(or, respectively, on  ) defines, for any piecewise-smooth curve
) defines, for any piecewise-smooth curve  in
in  , an isomorphic mapping
, an isomorphic mapping  between the fibres corresponding to the beginning and the end of
between the fibres corresponding to the beginning and the end of  . To each piecewise-smooth closed curve
. To each piecewise-smooth closed curve  in
in  beginning and ending at a point
beginning and ending at a point 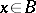 corresponds an automorphism of the fibre
corresponds an automorphism of the fibre  (or, respectively,
(or, respectively,  ) over the point
) over the point  . These automorphisms form a Lie group
. These automorphisms form a Lie group  , which is called the holonomy group of the connection
, which is called the holonomy group of the connection  at
at  .
.
If the base is (pathwise) connected, then 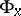 and
and  are isomorphic for any
are isomorphic for any  and
and  in
in  . One may accordingly speak of the holonomy group of a bundle
. One may accordingly speak of the holonomy group of a bundle 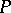 (or
(or 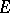 ) with connection
) with connection  and with (pathwise) connected base.
and with (pathwise) connected base.
The holonomy group 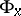 is a subgroup of the structure group
is a subgroup of the structure group  . In the case of a linear connection on
. In the case of a linear connection on 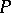 this subgroup may be defined directly. Let a point
this subgroup may be defined directly. Let a point 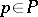 in the fibre
in the fibre 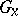 over a point
over a point  be given. The set of elements
be given. The set of elements 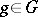 such that the points
such that the points 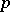 and
and  can be connected by horizontal curves in
can be connected by horizontal curves in  forms a subgroup
forms a subgroup  of
of  , which is isomorphic to
, which is isomorphic to 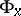 .
.
The limited (restricted) holonomy group  is the subgroup of the holonomy group
is the subgroup of the holonomy group  generated by the closed curves that are homotopic to zero. It coincides with the pathwise-connected component of the unit element of
generated by the closed curves that are homotopic to zero. It coincides with the pathwise-connected component of the unit element of  ; moreover,
; moreover,  is at most countable.
is at most countable.
The role of holonomy groups in the differential geometry of fibre bundles is explained by the following theorems on connections on  .
.
Reduction theorem. Let 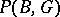 be a principal fibre bundle satisfying the second axiom of countability; let
be a principal fibre bundle satisfying the second axiom of countability; let 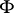 be the holonomy group of the connection
be the holonomy group of the connection  defined on
defined on 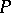 . Then the structure group
. Then the structure group 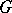 is reducible to its subgroup
is reducible to its subgroup  , and the connection
, and the connection  is reducible to a connection on the reduced fibre bundle
is reducible to a connection on the reduced fibre bundle  , the holonomy group of which coincides with
, the holonomy group of which coincides with  .
.
Holonomy theorem. The holonomy algebra (the algebra of the restricted holonomy group) is a subalgebra of the algebra of 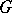 generated by all vectors
generated by all vectors 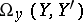 , where
, where  is the curvature form at the point
is the curvature form at the point  , where
, where 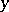 runs through the set of points which may be connected with the beginning point
runs through the set of points which may be connected with the beginning point  by a horizontal path, and
by a horizontal path, and 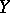 and
and 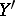 are arbitrary horizontal vectors.
are arbitrary horizontal vectors.
References
| [1] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [2] | R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) |
| [3] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
Holonomy group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Holonomy_group&oldid=12095