Holomorphic envelope
envelope of holomorphy, of a (Riemann) domain 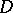
The largest domain 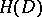 with the following property: Any holomorphic function in
with the following property: Any holomorphic function in 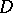 can be holomorphically continued to
can be holomorphically continued to 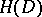 . The problem of constructing the envelope of holomorphy for a given domain
. The problem of constructing the envelope of holomorphy for a given domain 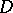 arises in connection with the fact that in a complex space
arises in connection with the fact that in a complex space 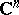 ,
, 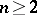 , not all domains are domains of holomorphy (cf. Domain of holomorphy), i.e. there exist domains such that any function that is holomorphic in this domain has a holomorphic continuation to a larger (usually not single-layered) domain. The envelope of holomorphy
, not all domains are domains of holomorphy (cf. Domain of holomorphy), i.e. there exist domains such that any function that is holomorphic in this domain has a holomorphic continuation to a larger (usually not single-layered) domain. The envelope of holomorphy 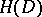 is a domain of holomorphy; if
is a domain of holomorphy; if 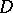 is a domain of holomorphy, then
is a domain of holomorphy, then 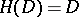 .
.
In applications in axiomatic quantum field theory there arises the non-trivial problem of constructing envelopes of holomorphy of a special kind, which reflect the physical requirements of spectrality, local commutativity and Lorentz covariance. The Bogolyubov theorem on the edge-of-the-wedge and continuity theorems (cf. Continuity theorem) are especially useful in this connection.
References
| [1] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
References
| [a1] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) pp. Chapt. 1, Sect. G |
Holomorphic envelope. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Holomorphic_envelope&oldid=13411