Holomorph of a group
A concept in group theory which arose in connection with the following problem. Is it possible to include any given group 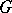 as a normal subgroup in some other group so that all the automorphisms of
as a normal subgroup in some other group so that all the automorphisms of 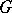 are restrictions of inner automorphisms of this large group? To solve a problem of this kind, a new group
are restrictions of inner automorphisms of this large group? To solve a problem of this kind, a new group 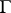 is constructed using
is constructed using 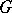 and its automorphism group
and its automorphism group 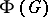 . The elements of
. The elements of 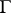 are pairs
are pairs 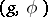 where
where 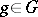 ,
, 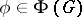 , and composition of pairs is defined by the formula
, and composition of pairs is defined by the formula
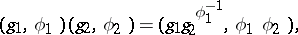 |
where 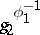 is the image of
is the image of 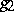 under
under  . The group
. The group 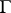 (or a group isomorphic to it) is called the holomorph of
(or a group isomorphic to it) is called the holomorph of 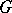 . The set of pairs of the form
. The set of pairs of the form 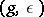 , where
, where  is the identity element of
is the identity element of 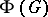 , constitutes a subgroup that is isomorphic to the original group
, constitutes a subgroup that is isomorphic to the original group 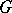 . In a similar manner, the pairs of the form
. In a similar manner, the pairs of the form  , where
, where  is the identity element of
is the identity element of 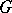 , constitute a subgroup isomorphic to the group
, constitute a subgroup isomorphic to the group  . The formula
. The formula
 |
shows that  is in fact a solution of the problem posed above.
is in fact a solution of the problem posed above.
Comments
References
| [a1] | M. Hall jr., "The theory of groups" , Macmillan (1959) |
| [a2] | A.G. Kurosh, "Theory of groups" , 1 , Chelsea (1955) (Translated from Russian) |
Holomorph of a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Holomorph_of_a_group&oldid=12406