Hodge conjecture
The statement that for any smooth projective variety  over the field
over the field  of complex numbers and for any integer
of complex numbers and for any integer  the
the  -space
-space  , where
, where  is the component of type
is the component of type  in the Hodge decomposition
in the Hodge decomposition
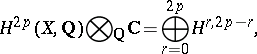 |
is generated by the cohomology classes of algebraic cycles of codimension  over
over  . This conjecture was put forth by W.V.D. Hodge in [1].
. This conjecture was put forth by W.V.D. Hodge in [1].
In the case  , the Hodge conjecture is equivalent to the Lefschetz theorem on cohomology of type
, the Hodge conjecture is equivalent to the Lefschetz theorem on cohomology of type  . The Hodge conjecture has also been proved for the following classes of varieties:
. The Hodge conjecture has also been proved for the following classes of varieties:
1)  is a smooth four-dimensional uniruled variety, that is, a variety such that there exists a rational mapping of finite degree
is a smooth four-dimensional uniruled variety, that is, a variety such that there exists a rational mapping of finite degree  , where
, where 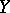 is a smooth variety (see [2]). Uniruled varieties are, for example, the unirational varieties and the four-dimensional complete intersections with an ample anti-canonical class (see [3]).
is a smooth variety (see [2]). Uniruled varieties are, for example, the unirational varieties and the four-dimensional complete intersections with an ample anti-canonical class (see [3]).
2) 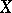 is a smooth Fermat hypersurface of prime order (see [4], [5]).
is a smooth Fermat hypersurface of prime order (see [4], [5]).
3)  is a simple five-dimensional Abelian variety (see [6]).
is a simple five-dimensional Abelian variety (see [6]).
4)  is a simple
is a simple 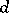 -dimensional Abelian variety, and
-dimensional Abelian variety, and  , where
, where 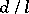 is an odd number, or
is an odd number, or 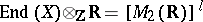 , where
, where  is an odd number.
is an odd number.
References
| [1] | W.V.D. Hodge, "The topological invariants of algebraic varieties" , Proc. Internat. Congress Mathematicians (Cambridge, 1950) , 1 , Amer. Math. Soc. (1952) pp. 182–192 |
| [2] | A. Conte, J.P. Murre, "The Hodge conjecture for fourfolds admitting a covering by rational curves" Math. Ann. , 238 (1978) pp. 79–88 |
| [3] | A. Conte, J.P. Murre, "The Hodge conjecture for Fano complete intersections of dimension four" , J. de Géométrie Algébrique d'Angers, juillet 1979 , Sijthoff & Noordhoff (1980) pp. 129–141 |
| [4] | Z. Ran, "Cycles on Fermat hypersurfaces" Compositio Math. , 42 : 1 (1980–1981) pp. 121–142 |
| [5] | T. Shioda, "The Hodge conjecture and the Tate conjecture for Fermat varieties" Proc. Japan. Acad. Ser. A , 55 : 3 (1979) pp. 111–114 |
| [6] | S.G. Tankeev, "On algebraic cycles on simple  -dimensional abelian varieties" Math. USSR Izv. , 19 (1982) pp. 95–123 Izv. Akad. Nauk SSSR Ser. Mat. , 45 : 4 (1981) pp. 793–823 -dimensional abelian varieties" Math. USSR Izv. , 19 (1982) pp. 95–123 Izv. Akad. Nauk SSSR Ser. Mat. , 45 : 4 (1981) pp. 793–823 |
Comments
A Hodge class on a smooth complex projective variety  is an element of
is an element of 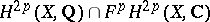 for some
for some  , where
, where 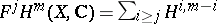 (the Hodge filtration, cf. Hodge structure). The Hodge conjecture regards the algebraicity of the Hodge classes.
(the Hodge filtration, cf. Hodge structure). The Hodge conjecture regards the algebraicity of the Hodge classes.
A weaker form is the variational Hodge conjecture. Suppose one has a smooth family of complex projective varieties and a locally constant cohomology class in the fibres which is everywhere a Hodge class and is algebraic at one fibre. Then it should be algebraic in nearby fibres. This has been verified in certain cases [a1], [a2].
An absolute Hodge class on a projective variety over a number field is a certain compatible system of cohomology classes in Betti, de Rham and étale cohomology. On an Abelian variety, every Hodge class is a Betti component of an absolute Hodge class [a3]. Absolute Hodge classes are used to define a weak notion of motif for algebraic varieties.
Hodge has formulated a more general conjecture, corrected by A. Grothendieck [a4]. Let  be a smooth complex projective variety. Suppose that
be a smooth complex projective variety. Suppose that  is a Hodge substructure such that
is a Hodge substructure such that  for
for 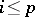 . Then there should exist an algebraic subset
. Then there should exist an algebraic subset  of
of  of codimension
of codimension  such that
such that 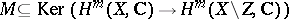 .
.
More general conjectures of this type are due to A. Beilinson [a5].
References
| [a1] | S. Bloch, "Semi-regularity and de Rham cohomology" Invent. Mat. , 17 (1972) pp. 51–66 |
| [a2] | J.H.M. Steenbrink, "Some remarks about the Hodge conjecture" E. Cattani (ed.) F. Guillán (ed.) A. Kaplan (ed.) et al. (ed.) , Hodge theory , Lect. notes in math. , 1246 , Springer pp. 165–175 |
| [a3] | P. Deligne (ed.) J.S. Milne (ed.) A. Ogus (ed.) K. Shih (ed.) , Hodge cycles, motives and Shimura varieties , Lect. notes in math. , 900 , Springer (1982) |
| [a4] | A. Grothendieck, "Hodge's general conjecture is false for trivial reasons" Topology , 8 (1969) pp. 299–303 |
| [a5] | A.A. Beilinson, "Notes on absolute Hodge cohomology" Contemp. Math. , 55 : 1 (1986) pp. 35–68 |
Hodge conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hodge_conjecture&oldid=16196