Hilbert system of axioms
for Euclidean geometry
A system of axioms proposed by D. Hilbert [1] in 1899, and subsequently amended and made more precise by him.
In Hilbert's system of axioms the primary (undefined) notions are points, straight lines, planes, and the relations between them are expressed by the words "belongs to" , "between in the Hilbert system of axiomsbetween" and "congruence in geometrycongruent to in the Hilbert system of axiomscongruent to" . The nature of the primary objects and the relations between those objects are arbitrary as long as the objects and the relations satisfy the axioms.
Hilbert's system contains 20 axioms, which are subdivided into five groups.
Group 
comprises eight incidence axioms which describe the relation "belonging" .
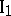 . For any two points there exists a straight line passing through them.
. For any two points there exists a straight line passing through them.
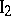 . There exists only one straight line passing through any two distinct points.
. There exists only one straight line passing through any two distinct points.
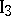 . At least two points lie on any straight line. There exist at least three points not lying on the same straight line.
. At least two points lie on any straight line. There exist at least three points not lying on the same straight line.
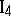 . There exists a plane passing through any three points not lying on the same straight line. At least one point lies on any given plane.
. There exists a plane passing through any three points not lying on the same straight line. At least one point lies on any given plane.
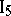 . There exists only one plane passing through any three points not lying on the same straight line.
. There exists only one plane passing through any three points not lying on the same straight line.
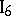 . If two points
. If two points 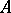 and
and 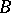 of a straight line
of a straight line  lie in a plane
lie in a plane  , then all points of
, then all points of  lie in
lie in 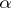 .
.
 . If two planes have one point in common, then they have at least one more point in common.
. If two planes have one point in common, then they have at least one more point in common.
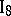 . There exist at least four points not lying in the same plane.
. There exist at least four points not lying in the same plane.
Group 
comprises four order axioms describing the relation "between" .
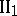 . If a point
. If a point 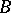 lies between a point
lies between a point 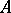 and a point
and a point  , then
, then 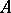 ,
, 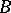 and
and 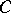 are distinct points on the same straight line and
are distinct points on the same straight line and 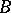 also lies between
also lies between 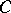 and
and 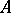 .
.
 . For any two points
. For any two points 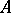 and
and 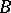 on the straight line
on the straight line 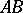 there exists at least one point
there exists at least one point 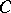 such that the point
such that the point 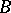 lies between
lies between 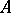 and
and  .
.
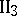 . Out of any three points on the same straight line there exists not more than one point lying between the other two.
. Out of any three points on the same straight line there exists not more than one point lying between the other two.
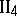 (Pasch's axiom). Let
(Pasch's axiom). Let 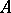 ,
, 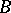 and
and 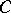 be three points not lying on the same straight line, and let
be three points not lying on the same straight line, and let  be a straight line in the plane
be a straight line in the plane 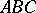 not passing through any of the points
not passing through any of the points  ,
,  or
or 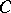 . Then, if the straight line
. Then, if the straight line  passes through an interior point of the segment
passes through an interior point of the segment 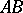 , it also passes through an interior point of the segment
, it also passes through an interior point of the segment 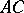 or through an interior point of the segment
or through an interior point of the segment  .
.
Group 
comprises five axioms of congruence, which describe the relation of "being congruent" (Hilbert denoted this relation by the symbol  ).
).
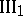 . Given a segment
. Given a segment 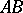 and a ray
and a ray  , there exists a point
, there exists a point 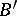 on
on 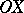 such that the segment
such that the segment 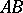 is congruent to the segment
is congruent to the segment 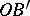 , i.e.
, i.e. 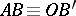 .
.
 . If
. If 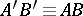 and
and 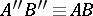 , then
, then 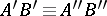 .
.
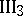 . Let
. Let 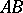 and
and 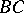 be two segments on a straight line without common interior points, and let
be two segments on a straight line without common interior points, and let 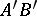 and
and 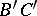 be two segments on the same or on a different straight line, also without any common interior points. If
be two segments on the same or on a different straight line, also without any common interior points. If 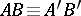 and
and 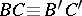 , then
, then 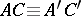 .
.
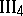 . Let there be given an angle
. Let there be given an angle 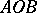 , a ray
, a ray 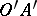 and a half-plane
and a half-plane 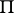 bounded by the straight line
bounded by the straight line 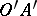 . Then
. Then 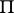 contains one and only one ray
contains one and only one ray 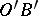 such that
such that 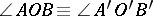 . Moreover, every angle is congruent to itself.
. Moreover, every angle is congruent to itself.
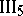 . If for two triangles
. If for two triangles  and
and 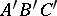 one has
one has 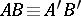 ,
, 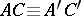 ,
, 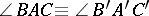 , then
, then 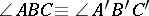 .
.
Group 
comprises two continuity axioms.
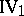 (Archimedes' axiom). Let
(Archimedes' axiom). Let 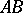 and
and 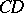 be two arbitrary segments. Then the straight line
be two arbitrary segments. Then the straight line 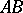 contains a finite set of points
contains a finite set of points 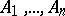 such that the point
such that the point 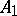 lies between
lies between 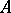 and
and 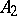 , the point
, the point 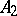 lies between
lies between 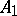 and
and 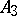 , etc., and such that the segments
, etc., and such that the segments 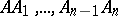 are congruent to the segment
are congruent to the segment  , and
, and 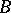 lies between
lies between 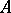 and
and 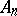 .
.
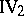 (Cantor's axiom). Let there be given, on any straight line
(Cantor's axiom). Let there be given, on any straight line  , an infinite sequence of segments
, an infinite sequence of segments 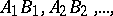 which satisfies two conditions: a) each segment in the sequence forms a part of the segment which precedes it; b) for each preassigned segment
which satisfies two conditions: a) each segment in the sequence forms a part of the segment which precedes it; b) for each preassigned segment 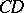 it is possible to find a natural number
it is possible to find a natural number  such that
such that 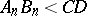 . Then
. Then  contains a point
contains a point 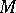 belonging to all the segments of this sequence.
belonging to all the segments of this sequence.
Group 
comprises one axiom about parallels. Let there be given a straight line  and a point
and a point 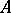 not on that straight line. Then there exists not more than one straight line passing through
not on that straight line. Then there exists not more than one straight line passing through 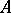 , not intersecting
, not intersecting  and lying in the plane defined by
and lying in the plane defined by  and
and 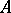 .
.
(Hilbert classified the axiom about parallels in Group IV, and the continuity axioms in Group V).
All other axioms of Euclidean geometry are defined by the basic concepts of Hilbert's system of axioms, while all the statements regarding the properties of geometrical figures and not included in Hilbert's system must be logically deducible from the axioms, or from statements which are deducible from these axioms.
Hilbert's system of axioms is complete; it is consistent if the arithmetic of real numbers is consistent. If, in Hilbert's system, the axiom about parallels is replaced by its negation, the new system of axioms thus obtained is also consistent (the system of axioms of Lobachevskii geometry), which means that the axiom about parallels is independent of the other axioms in Hilbert's system. It is also possible to demonstrate that some other axioms of this system are independent of the others.
Hilbert's system of axioms is the first fairly rigorous foundation of Euclidean geometry.
References
| [1] | D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968) |
| [2] | N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) |
Comments
In axiom 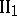 the point
the point 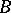 is also called an interior point of the segment
is also called an interior point of the segment 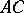 (Pasch's axiom should be read with this in mind).
(Pasch's axiom should be read with this in mind).
Also, Hilbert originally used different continuity axioms: the Archimedean axiom and a completeness axiom of his own.
References
| [a1] | H.G. Forder, "Foundations of Euclidean geometry" , Dover, reprint (1958) |
| [a2] | A.D. Aleksandrov, "Foundations of geometry" Siberian Math. J. , 28 (1987) pp. 523–539 Sibirsk. Mat. Zh. , 28 (1987) pp. 9–28 |
Hilbert system of axioms. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_system_of_axioms&oldid=13772