Hilbert-Schmidt integral operator
A bounded linear integral operator 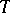 acting from the space
acting from the space 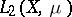 into
into 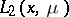 and representable in the form
and representable in the form
 |
where 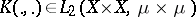 is the kernel of the operator (cf. Kernel of an integral operator, [1]).
is the kernel of the operator (cf. Kernel of an integral operator, [1]).
D. Hilbert and E. Schmidt in 1907 were the first to study operators of this kind. A Hilbert–Schmidt integral operator is a completely-continuous operator [2]. Its adjoint is also a Hilbert–Schmidt integral operator, with kernel  [3]. A Hilbert–Schmidt integral operator is a self-adjoint operator if and only if
[3]. A Hilbert–Schmidt integral operator is a self-adjoint operator if and only if  for almost-all
for almost-all 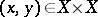 (with respect to
(with respect to 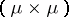 ). For a self-adjoint Hilbert–Schmidt integral operator and for its kernel the following expansions are valid:
). For a self-adjoint Hilbert–Schmidt integral operator and for its kernel the following expansions are valid:
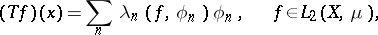 | (1) |
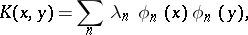 | (2) |
where 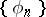 is the orthonormal system of eigen functions of
is the orthonormal system of eigen functions of 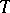 corresponding to the eigen values
corresponding to the eigen values 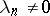 . The series (1) converges with respect to the norm of
. The series (1) converges with respect to the norm of 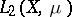 , while the series (2) converges with respect to the norm of
, while the series (2) converges with respect to the norm of 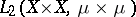 , [4]. Under the conditions of the Mercer theorem the series (2) converges absolutely and uniformly [5].
, [4]. Under the conditions of the Mercer theorem the series (2) converges absolutely and uniformly [5].
If
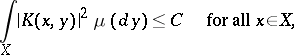 |
then the series (1) converges absolutely and uniformly, [4].
If 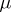 is a
is a 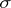 -finite measure, then the linear operator
-finite measure, then the linear operator
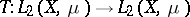 |
is a Hilbert–Schmidt integral operator if and only if there exists a function 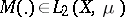 such that the inequality
such that the inequality
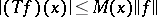 |
is valid for almost-all 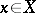 (with respect to the measure
(with respect to the measure 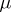 ) [7]. Thus, the Hilbert–Schmidt integral operators form a two-sided ideal in the Banach algebra of all bounded linear operators acting from
) [7]. Thus, the Hilbert–Schmidt integral operators form a two-sided ideal in the Banach algebra of all bounded linear operators acting from 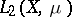 into
into 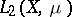 .
.
Hilbert–Schmidt integral operators play an important role in the theory of integral equations and in the theory of boundary value problems [8], [9], because the operators which appear in many problems of mathematical physics are either themselves Hilbert–Schmidt integral operators or else their iteration to a certain order is such an operator. A natural generalization of a Hilbert–Schmidt integral operator is a Hilbert–Schmidt operator.
References
| [1] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963) |
| [2] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1 |
| [3] | M.H. Stone, "Linear transformations in Hilbert space and their applications to analysis" , Amer. Math. Soc. (1932) |
| [4] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
| [5] | J.A. Dieudonné, "Foundations of modern analysis" , Acad. Press (1961) (Translated from French) |
| [6] | L.V. Kantorovich, B.Z. Vulikh, A.G. Pinsker, "Functional analysis in semi-ordered spaces" , Moscow-Leningrad (1950) (In Russian) |
| [7] | J. Weidmann, "Carleman operatoren" Manuscripta Math. , 2 : 1 (1970) pp. 1–38 |
| [8] | K. Moren, "Methods of Hilbert spaces" , PWN (1967) (Translated from Polish) |
| [9] | Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian) |
Comments
References
| [a1] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1977) |
| [a2] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1981) (Translated from Russian) |
Hilbert-Schmidt integral operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert-Schmidt_integral_operator&oldid=12345