Hessian of a function
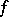
The quadratic form
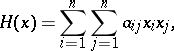 |
or
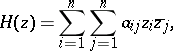 |
where 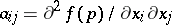 (or
(or 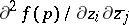 ) and
) and 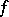 is given on the
is given on the  -dimensional real space
-dimensional real space 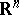 (or on the complex space
(or on the complex space 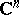 ) with coordinates
) with coordinates  (or
(or  ). Introduced in 1844 by O. Hesse. With the aid of a local coordinate system this definition is transferred to functions defined on a real manifold of class
). Introduced in 1844 by O. Hesse. With the aid of a local coordinate system this definition is transferred to functions defined on a real manifold of class 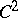 (or on a complex space), at critical points of the functions. In both cases the Hessian is a quadratic form given on the tangent space and is independent of the choice of coordinates. In Morse theory the Hessian is used to define the concepts of a (non-)degenerate critical point, the Morse form and the Bott form. In complex analysis the Hessian is used in the definition of a pseudo-convex space (cf. Pseudo-convex and pseudo-concave) and of a plurisubharmonic function.
(or on a complex space), at critical points of the functions. In both cases the Hessian is a quadratic form given on the tangent space and is independent of the choice of coordinates. In Morse theory the Hessian is used to define the concepts of a (non-)degenerate critical point, the Morse form and the Bott form. In complex analysis the Hessian is used in the definition of a pseudo-convex space (cf. Pseudo-convex and pseudo-concave) and of a plurisubharmonic function.
References
| [1] | M.M. Postnikov, "Introduction to Morse theory" , Moscow (1971) (In Russian) |
| [2] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
Comments
One usually calls the form 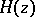 on
on 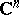 the complex Hessian.
the complex Hessian.
If the Hessian of a real-valued function is a positive (semi-) definite form, then the function is convex; similarly, if the complex Hessian of a function is a positive (semi-) definite form, then the function is plurisubharmonic.
References
| [a1] | S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) pp. Chapt. 3 |
Hessian of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hessian_of_a_function&oldid=19311