Hermitian matrix

Hermitian-symmetric matrix, self-conjugate matrix

A square matrix over that is the same as its Hermitian-conjugate matrix

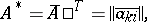that is, a matrix whose entries satisfy the condition . If all the , then a Hermitian matrix is symmetric (cf. Symmetric matrix). The Hermitian matrices of a fixed order form a vector space over . If and are two Hermitian matrices of the same order, then so is . Under the operation the Hermitian matrices (of order ) form a Jordan algebra. The product 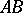of two Hermitian matrices is itself Hermitian if and only if 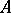and commute.

The Hermitian matrices of order are the matrices of Hermitian transformations of an -dimensional unitary space in an orthonormal basis (see Self-adjoint linear transformation). On the other hand, Hermitian matrices are the matrices of Hermitian forms in an -dimensional complex vector space. Like Hermitian forms (cf. Hermitian form), Hermitian matrices can be defined over any skew-field with an anti-involution.

All eigen values of a Hermitian matrix are real. For every Hermitian matrix 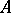there exists a unitary matrix 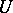such that is a real diagonal matrix. A Hermitian matrix is called non-negative (or positive semi-definite) if all its principal minors are non-negative, and positive definite if they are all positive. Non-negative (positive-definite) Hermitian matrices correspond to non-negative (positive-definite) Hermitian linear transformations and Hermitian forms.

References

[a1]	F.R. [F.R. Gantmakher] Gantmacher, "Matrix theory" , 1–2 , Chelsea, reprint (1959) (Translated from Russian)
[a2]	B. Noble, J.W. Daniel, "Applied linear algebra" , Prentice-Hall (1979)