Hermitian form
on a left  -module
-module 
A mapping  that is linear in the first argument and satisfies the condition
that is linear in the first argument and satisfies the condition
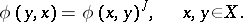 |
Here  is a ring with a unit element and equipped with an involutory anti-automorphism
is a ring with a unit element and equipped with an involutory anti-automorphism  . In particular,
. In particular,  is a sesquilinear form on
is a sesquilinear form on  . The module
. The module 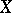 itself is then called a Hermitian space. By analogy with what is done for bilinear forms, equivalence is defined for Hermitian forms (in another terminology, isometry) and, correspondingly, isomorphism (isometry) of Hermitian spaces (in particular, automorphism). All automorphisms of a Hermitian form
itself is then called a Hermitian space. By analogy with what is done for bilinear forms, equivalence is defined for Hermitian forms (in another terminology, isometry) and, correspondingly, isomorphism (isometry) of Hermitian spaces (in particular, automorphism). All automorphisms of a Hermitian form 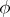 form a group
form a group 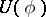 , which is called the unitary group associated with the Hermitian form
, which is called the unitary group associated with the Hermitian form 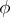 ; its structure has been well studied when
; its structure has been well studied when 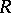 is a skew-field (see Unitary group).
is a skew-field (see Unitary group).
A Hermitian form is a special case of an  -Hermitian form (where
-Hermitian form (where  is an element in the centre of
is an element in the centre of 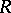 ), that is, a sesquilinear form
), that is, a sesquilinear form  on
on 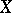 for which
for which
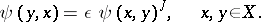 |
When 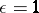 , an
, an  -Hermitian form is Hermitian, and when
-Hermitian form is Hermitian, and when 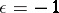 the form is called skew-Hermitian or anti-Hermitian. If
the form is called skew-Hermitian or anti-Hermitian. If 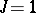 , a Hermitian form is a symmetric bilinear form, and a skew-Hermitian form is a skew-symmetric or anti-symmetric bilinear form. If the mapping
, a Hermitian form is a symmetric bilinear form, and a skew-Hermitian form is a skew-symmetric or anti-symmetric bilinear form. If the mapping
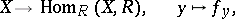 |
where 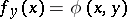 for any
for any 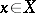 , is bijective, then
, is bijective, then 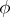 is called a non-degenerate Hermitian form or a Hermitian scalar product on
is called a non-degenerate Hermitian form or a Hermitian scalar product on 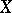 .
.
If 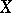 is a free
is a free 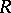 -module with a basis
-module with a basis  , then the matrix
, then the matrix 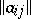 , where
, where  , is called the matrix of
, is called the matrix of 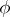 in the given basis; it is a Hermitian matrix (that is,
in the given basis; it is a Hermitian matrix (that is, 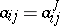 ). A Hermitian form
). A Hermitian form 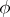 is non-degenerate if and only if
is non-degenerate if and only if 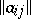 is invertible. If
is invertible. If 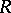 is a skew-field, if
is a skew-field, if 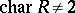 , and if
, and if 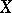 is finite-dimensional over
is finite-dimensional over 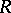 , then
, then 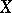 has an orthogonal basis relative to
has an orthogonal basis relative to 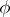 (in which the matrix is diagonal).
(in which the matrix is diagonal).
If 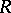 is a commutative ring with identity, if
is a commutative ring with identity, if 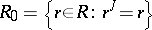 , and if the matrix of
, and if the matrix of 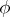 is definite, then its determinant lies in
is definite, then its determinant lies in 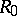 . Under a change of basis in
. Under a change of basis in 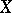 this determinant is multiplied by a non-zero element of
this determinant is multiplied by a non-zero element of 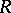 of the form
of the form 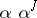 , where
, where 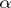 is an invertible element of
is an invertible element of 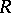 . The determinant regarded up to multiplication by such elements is called the determinant of the Hermitian form or of the Hermitian space
. The determinant regarded up to multiplication by such elements is called the determinant of the Hermitian form or of the Hermitian space 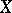 ; it is an important invariant and is used in the classification of Hermitian forms.
; it is an important invariant and is used in the classification of Hermitian forms.
Let 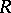 be commutative. Then a Hermitian form
be commutative. Then a Hermitian form 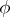 on
on 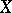 gives rise to a quadratic form
gives rise to a quadratic form 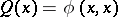 on
on 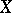 over
over 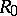 . The analysis of such forms lies at the basis of the construction of the Witt group of
. The analysis of such forms lies at the basis of the construction of the Witt group of 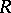 with an involution (see Witt ring; Witt decomposition; Witt theorem). When
with an involution (see Witt ring; Witt decomposition; Witt theorem). When 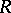 is a maximal ordered field, then the law of inertia extends to Hermitian forms (and there arise the corresponding concepts of the signature, the index of inertia, and positive and negative definiteness). If
is a maximal ordered field, then the law of inertia extends to Hermitian forms (and there arise the corresponding concepts of the signature, the index of inertia, and positive and negative definiteness). If 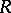 is a field and
is a field and 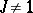 , then
, then 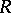 is a quadratic Galois extension of
is a quadratic Galois extension of  , and isometry of two non-degenerate Hermitian forms over
, and isometry of two non-degenerate Hermitian forms over 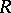 is equivalent to isometry of the quadratic forms over
is equivalent to isometry of the quadratic forms over 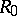 generated by them; this reduces the classification of non-degenerate Hermitian forms over
generated by them; this reduces the classification of non-degenerate Hermitian forms over 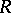 to that of non-degenerate quadratic forms over
to that of non-degenerate quadratic forms over 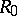 .
.
If 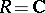 and
and  is the involution of complex conjugation, then a complete system of invariants of Hermitian forms over a finite-dimensional space is given by the rank and the signature of the corresponding quadratic forms. If
is the involution of complex conjugation, then a complete system of invariants of Hermitian forms over a finite-dimensional space is given by the rank and the signature of the corresponding quadratic forms. If  is a local field or the field of functions of a single variable over a finite field, then a complete system of invariants for non-degenerate Hermitian forms is given by the rank and the determinant. If
is a local field or the field of functions of a single variable over a finite field, then a complete system of invariants for non-degenerate Hermitian forms is given by the rank and the determinant. If 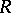 is a finite field, then there is only one invariant, the rank. For the case when
is a finite field, then there is only one invariant, the rank. For the case when 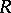 is an algebraic extension of
is an algebraic extension of 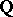 , see [3]. Ch. Hermite was the first, in 1853, to consider the forms that bear his name in connection with certain problems of number theory.
, see [3]. Ch. Hermite was the first, in 1853, to consider the forms that bear his name in connection with certain problems of number theory.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [2] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
| [3] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) |
| [4] | O.T. O'Meara, "Introduction to quadratic forms" , Springer (1973) |
Hermitian form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermitian_form&oldid=14638