Hermite polynomials
Chebyshev–Hermite polynomials
Polynomials orthogonal on  with the weight function
with the weight function  . The standardized Hermite polynomials are defined by the Rodrigues formula
. The standardized Hermite polynomials are defined by the Rodrigues formula
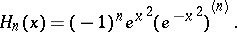 |
The most commonly used formulas are:
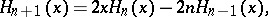 |
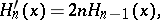 |
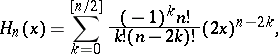 |
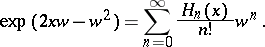 |
The first few Hermite polynomials are:
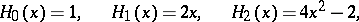 |
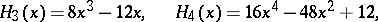 |
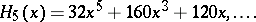 |
The polynomial 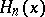 satisfies the differential equation
satisfies the differential equation
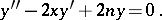 |
The orthonormal Hermite polynomials are defined by
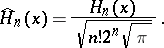 |
The Hermite polynomials with leading coefficient one have the form
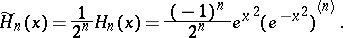 |
Fourier series in Hermite polynomials in the interior of 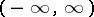 behave analogous to trigonometric Fourier series.
behave analogous to trigonometric Fourier series.
In mathematical statistics and probability theory one uses the Hermite polynomials corresponding to the weight function
 |
The definition of Hermite polynomials is encountered in P. Laplace [1]. A detailed study of them was published by P.L. Chebyshev in 1859 (see [2]). Later, these polynomials were studied by Ch. Hermite . V.A. Steklov [4] proved that the set of them is dense in the space of square-summable functions with the weight  on the whole real line.
on the whole real line.
References
| [1] | P.S. Laplace, Mém. Cl. Sci. Math. Phys. Inst. France , 58 (1810) pp. 279–347 |
| [2] | P.L. Chebyshev, , Collected works , 2 , Moscow-Leningrad (1947) pp. 335–341 (In Russian) |
| [3a] | Ch. Hermite, C.R. Acad. Sci. Paris , 58 (1864) pp. 93–100 |
| [3b] | Ch. Hermite, C.R. Acad. Sci. Paris , 58 (1864) pp. 266–273 |
| [4] | V.A. Steklov, Izv. Akad. Nauk , 10 (1956) pp. 403–416 |
| [5] | P.K. Suetin, "Classical orthogonal polynomials" , Moscow (1979) (In Russian) |
Comments
The result by Steklov mentioned in the last sentence of the main article goes back at least to H. Weyl (1908), cf. the references in [a3], Sect. 5.7.
One possible way to prove the Plancherel formula for the Fourier transform is by use of Hermite polynomials, cf. [a4]. Hermite polynomials occur in solutions of the heat and Schrödinger equations and in the so-called heat polynomials, cf. [a1]. A canonical orthonormal basis of the representation space for the Schrödinger representation of the Heisenberg group is given in terms of Hermite polynomials, cf. [a2].
References
| [a1] | W. Miller jr., "Symmetry and separation of variables" , Addison-Wesley (1977) |
| [a2] | W. Schempp, "Harmonic analysis on the Heisenberg nilpotent Lie group" , Longman (1986) |
| [a3] | G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975) |
| [a4] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) |
Hermite polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermite_polynomials&oldid=14720