Herglotz formula

An integral relation between two closed isometric oriented regular surfaces. Let local coordinates and be introduced on the surfaces 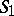and 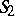so that equality of the coordinates realizes an isometric mapping. Let

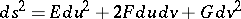be the first fundamental form, having the same coefficients for both surfaces in the given coordinates, let 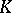be the Gaussian curvature, let 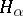be the mean curvatures, and let

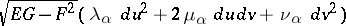be the second fundamental forms of the surfaces 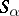. Herglotz' formula then takes the following form:

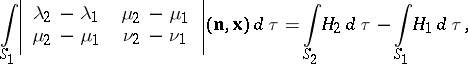where 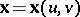is the position vector of 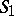, is the unit vector of the normal to 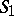and 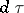is the surface element. It was obtained by G. Herglotz [1].

References

[1]	G. Herglotz, "Ueber die Starrheit von Eiflächen" Abh. Math. Sem. Univ. Hamburg , 15 (1943) pp. 127–129
[2]	N.V. Efimov, "Qualitative questions of the theory of deformations of surfaces" Uspekhi Mat. Nauk , 3 : 2 (1948) pp. 47–158 (In Russian)

Comments

This formula can be used to prove rigidity or congruence theorems for surfaces. For related formulas and results see [a1].

References

[a1]	H. Huck, R. Roitzsch, U. Simon, W. Vortisch, R. Walden, B. Wegner, W. Wendland, "Beweismethoden der Differentialgeometrie im Grossen" , Lect. notes in math. , 335 , Springer (1973)
[a2]	W. Klingenberg, "A course in differential geometry" , Springer (1978) (Translated from German)