Hensel lemma
A statement obtained by K. Hensel [1] in the creation of the theory of 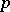 -adic numbers (cf.
-adic numbers (cf.  -adic number), which subsequently found extensive use in commutative algebra. One says that Hensel's lemma is valid for a local ring
-adic number), which subsequently found extensive use in commutative algebra. One says that Hensel's lemma is valid for a local ring 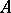 with maximal ideal
with maximal ideal 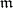 if for any unitary polynomial
if for any unitary polynomial  and decomposition
and decomposition 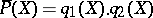 of its reduction modulo
of its reduction modulo 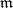 into a product of two mutually-prime polynomials
into a product of two mutually-prime polynomials
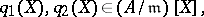 |
there exist polynomials
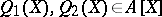 |
such that
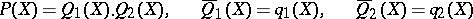 |
(here the bar denotes the image under the reduction 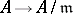 ). In particular, for any simple root
). In particular, for any simple root 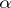 of the reduced polynomial
of the reduced polynomial 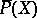 there exists a solution
there exists a solution 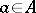 of the equation
of the equation 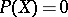 which satisfies the condition
which satisfies the condition 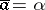 . Hensel's lemma is fulfilled, for example, for a complete local ring. Hensel's lemma makes it possible to reduce the solution of an algebraic equation over a complete local ring to the solution of the corresponding equation over its residue field. Thus, in the ring
. Hensel's lemma is fulfilled, for example, for a complete local ring. Hensel's lemma makes it possible to reduce the solution of an algebraic equation over a complete local ring to the solution of the corresponding equation over its residue field. Thus, in the ring 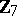 of
of 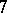 -adic numbers, Hensel's lemma yields the solvability of the equation
-adic numbers, Hensel's lemma yields the solvability of the equation 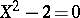 , since this equation has two simple roots in the field
, since this equation has two simple roots in the field 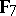 of seven elements. A local ring for which Hensel's lemma is valid is known as a Hensel ring.
of seven elements. A local ring for which Hensel's lemma is valid is known as a Hensel ring.
For Hensel's lemma in the non-commutative case see [3].
References
| [1] | K. Hensel, "Neue Grundlagen der Arithmetik" J. Reine Angew. Math. , 127 (1904) pp. 51–84 |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [3] | H. Zassenhaus, "Ueber eine Verallgemeinerung des Henselschen Lemmas" Arch. Math. (Basel) , 5 (1954) pp. 317–325 |
Hensel lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hensel_lemma&oldid=15048