Hellinger distance
From Encyclopedia of Mathematics
A distance between probability measures, expressed in terms of the Hellinger integral. Suppose that on a measurable space  a family of probability measures
a family of probability measures  ,
,  , is given that are all absolutely continuous relative to some
, is given that are all absolutely continuous relative to some  -finite measure
-finite measure  on
on  .
.
The Hellinger distance between two measures  and
and  (
( ) is defined by the formula
) is defined by the formula
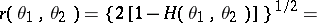 |
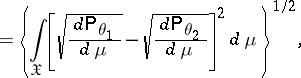 |
where
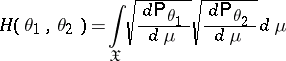 |
is the Hellinger integral. The Hellinger distance does not depend on the choice of the measure 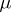 and has the following properties:
and has the following properties:
1) 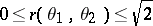 ;
;
2) 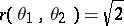 if and only if the measures
if and only if the measures 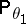 and
and 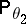 are mutually singular;
are mutually singular;
3) 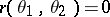 if and only if
if and only if 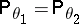 .
.
Let
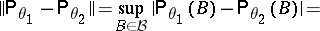 |
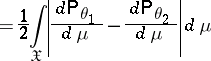 |
be the distance in variation between the measures 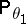 and
and 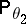 . Then
. Then
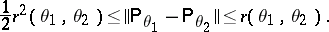 |
References
| [1] | H.H. Kuo, "Gaussian measures on Banach spaces" , Springer (1975) |
| [2] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [3] | I.A. Ibragimov, R.Z. [R.Z. Khas'minskii] Has'minskii, "Statistical estimation: asymptotic theory" , Springer (1981) (Translated from Russian) |
| [4] | V.M. Zolotarev, "Properties and relations of certain types of metrics" Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Akad. Nauk. USSR , 87 (1979) pp. 18–35; 206–212 (In Russian) (English summary) |
How to Cite This Entry:
Hellinger distance. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hellinger_distance&oldid=16453
Hellinger distance. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hellinger_distance&oldid=16453
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article