Heisenberg representation
One of the principal possible equivalent representations (together with the Schrödinger representation and the representation of interaction, cf. Interaction, representation of) of the dependence of the operators 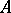 and the wave functions
and the wave functions 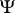 on the time
on the time 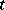 in quantum mechanics and in quantum field theory. In the Heisenberg representation the operators
in quantum mechanics and in quantum field theory. In the Heisenberg representation the operators 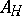 depend on
depend on 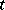 , while the wave functions
, while the wave functions 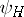 do not depend on
do not depend on 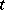 , and are connected with the corresponding
, and are connected with the corresponding 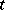 -independent operators
-independent operators 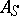 and
and 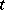 -dependent wave functions
-dependent wave functions 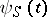 in the Schrödinger representation by a unitary transformation
in the Schrödinger representation by a unitary transformation
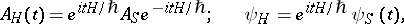 | (1) |
where the Hermitian operator 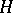 is the complete Hamiltonian of the system, which is independent of time. That it is possible to introduce the Heisenberg representation, the Schrödinger representation and the representation of interaction, and that they are equivalent, is due to the fact that it is not
is the complete Hamiltonian of the system, which is independent of time. That it is possible to introduce the Heisenberg representation, the Schrödinger representation and the representation of interaction, and that they are equivalent, is due to the fact that it is not 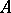 or
or 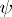 by themselves but only the average value of the operators
by themselves but only the average value of the operators 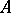 in the state
in the state 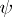 that must be invariant with respect to unitary transformations of the type (1) and, consequently, the average value should not depend on the selection of the representation. Differentiation of (1) with respect to
that must be invariant with respect to unitary transformations of the type (1) and, consequently, the average value should not depend on the selection of the representation. Differentiation of (1) with respect to  yields an equation for the operators
yields an equation for the operators 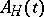 in the Heisenberg representation that contains complete information on the variation of the state of the quantum system with the time
in the Heisenberg representation that contains complete information on the variation of the state of the quantum system with the time 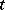 :
:
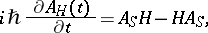 |
where the operators 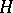 and
and 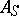 do not usually commute.
do not usually commute.
Named after W. Heisenberg, who introduced it in 1925 in a matrix formulation of quantum mechanics.
Comments
References
| [a1] | J. Mehra, H. Rechenberg, "The historical development of quantum theory" , 1–4 , Springer (1982) |
Heisenberg representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Heisenberg_representation&oldid=14131