Height, in Diophantine geometry
A certain numerical function on the set of solutions of a Diophantine equation (cf. Diophantine equations). In the simplest case of a solution in integers 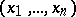 of a Diophantine equation, the height is a function of the solution, and equals
of a Diophantine equation, the height is a function of the solution, and equals  . It is encountered in this form in Fermat's method of descent. Let
. It is encountered in this form in Fermat's method of descent. Let  be a projective algebraic variety defined over a global field
be a projective algebraic variety defined over a global field 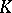 . The height is a class of real-valued functions
. The height is a class of real-valued functions 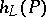 defined on the set
defined on the set 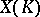 of rational points
of rational points 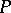 and depending on a morphism
and depending on a morphism 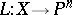 of the variety
of the variety 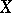 into the projective space
into the projective space 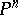 . Each function in this class is also called a height. From the point of view of estimating the number of rational points there are no essential differences between the functions in this class: for any two functions
. Each function in this class is also called a height. From the point of view of estimating the number of rational points there are no essential differences between the functions in this class: for any two functions 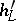 and
and 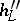 there exist constants
there exist constants 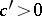 and
and 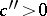 , such that
, such that 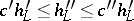 . Such functions are called equivalent, and this equivalence is denoted (here) as
. Such functions are called equivalent, and this equivalence is denoted (here) as 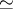 .
.
Fundamental properties of the height. The function 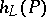 is functorial with respect to
is functorial with respect to 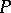 , i.e. for any morphism
, i.e. for any morphism 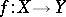 and morphism
and morphism  ,
,
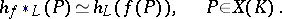 |
If the morphisms 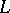 ,
, 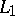 and
and 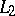 are defined by invertible sheaves
are defined by invertible sheaves 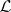 ,
,  and
and 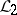 , and if
, and if 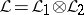 , then
, then 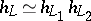 . The set of points
. The set of points 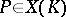 of bounded height is finite in the following sense: If the basic field
of bounded height is finite in the following sense: If the basic field 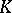 is an algebraic number field, the set is finite; if it is an algebraic function field with field of constants
is an algebraic number field, the set is finite; if it is an algebraic function field with field of constants 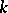 , the elements of
, the elements of  depend on a finite number of parameters from the field
depend on a finite number of parameters from the field 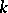 ; in particular,
; in particular, 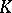 is finite if the field
is finite if the field 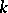 is finite. Let
is finite. Let 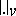 run through the set of all norms of
run through the set of all norms of 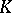 . One may then define the height of a point
. One may then define the height of a point 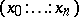 of the projective space
of the projective space 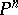 with coordinates from
with coordinates from 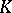 as
as
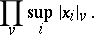 | (*) |
This is well defined because of the product formula 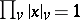 ,
,  . Let
. Let 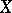 be an arbitrary projective variety over
be an arbitrary projective variety over 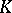 and let
and let 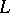 be a closed imbedding of
be a closed imbedding of 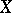 into the projective space; the height
into the projective space; the height 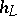 may then be obtained by transferring the function (*), using the imbedding, to the set
may then be obtained by transferring the function (*), using the imbedding, to the set 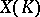 . Various projective imbeddings, corresponding to the same sheaf
. Various projective imbeddings, corresponding to the same sheaf 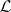 , define equivalent functions on
, define equivalent functions on 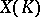 . A linear extension yields the desired function
. A linear extension yields the desired function 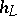 . The function
. The function  is occasionally replaced by its logarithm — the so-called logarithmic height.
is occasionally replaced by its logarithm — the so-called logarithmic height.
The above estimates may sometimes follow from exact equations [3], [4], [5]. There is a variant of the height function — the Néron–Tate height — which is defined on Abelian varieties and behaves as a functor with respect to the morphisms of Abelian varieties preserving the zero point. For the local aspect see [6]. The local components of a height constructed there play the role of intersection indices in arithmetic.
References
| [1] | A. Weil, "Number theory and algebraic geometry" , Proc. Internat. Congress Mathematicians (Cambridge, 1950) , 2 , Amer. Math. Soc. (1952) pp. 90–100 |
| [2] | S. Lang, "Diophantine geometry" , Interscience (1962) |
| [3] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) (Appendix in Russian translation: Yu.I. Manin; The Mordell–Weil theorem (in Russian)) |
| [4] | Yu.I. Manin, "Height of theta points on an Abelian manifold, their variants and applications" Izv. Akad. Nauk SSSR Ser. Mat. , 28 (1964) pp. 1363–1390 (In Russian) |
| [5] | D. Mumford, "A remark on Mordell's conjecture" Amer. J. Math. , 87 (1965) pp. 1007–1016 |
| [6] | A. Néron, "Quasi-fonctions et hauteurs sur les variétés abéliennes" Ann. of Math. (2) , 82 (1965) pp. 249–331 |
Comments
The notion of height is a major tool in arithmetic algebraic geometry. It plays an important role in Faltings' proof of the Tate conjecture on endomorphisms of Abelian varieties over number fields, the Shafarevich conjecture that there are only finitely many isomorphism classes of Abelian varieties over a number field over 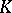 of given dimension
of given dimension 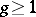 with good reduction outside a finite set of places
with good reduction outside a finite set of places 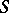 of
of 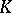 , and the Mordell conjecture on the finiteness of the set of rational points
, and the Mordell conjecture on the finiteness of the set of rational points  of a smooth curve of genus
of a smooth curve of genus 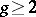 over a number field
over a number field 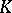 . Heights also play an important role in Arakelov intersection theory, which via moduli spaces of algebraic curves has also become important in string theory in mathematical physics.
. Heights also play an important role in Arakelov intersection theory, which via moduli spaces of algebraic curves has also become important in string theory in mathematical physics.
References
| [a1] | G. Faltings (ed.) G. Wüstholtz (ed.) , Rational points , Vieweg (1986) |
Height, in Diophantine geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Height,_in_Diophantine_geometry&oldid=18249