Heavy sphere, method of the
A method for solving a minimization problem for a differentiable function on a Euclidean space 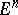 . The method is based on considering the system of differential equations
. The method is based on considering the system of differential equations
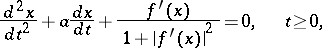 | (1) |
which describes the movement of a material point over the surface 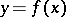 in an attracting field directed in the negative direction of the
in an attracting field directed in the negative direction of the 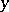 -axis under the condition that the point may not leave the surface and that the attraction is proportional to the velocity;
-axis under the condition that the point may not leave the surface and that the attraction is proportional to the velocity;  is de gradient of
is de gradient of 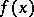 at a point
at a point  and
and  is the attraction coefficient. Taking into account that
is the attraction coefficient. Taking into account that 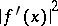 is small in a neighbourhood of a stationary point, (1) is often replaced by the system
is small in a neighbourhood of a stationary point, (1) is often replaced by the system
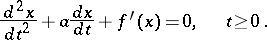 | (2) |
Subject to certain assumptions on 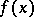 and under the initial conditions
and under the initial conditions
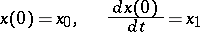 |
it can be shown that the corresponding solution 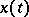 of (1) or (2), as
of (1) or (2), as  , converges to some stationary point
, converges to some stationary point  of
of 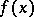 . If
. If 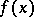 is a convex function, then
is a convex function, then 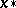 is a minimum point of it. Thus, the method of the heavy sphere is a particular case of the adjustment method. For the numerical solution of (1), or (2), one may, use, e.g., difference methods. In dependence on the choice of this difference method, discrete analogues of the method of the heavy sphere are obtained, including those for functions depending strongly on a few variables, the conjugate-gradient method, etc. (cf. Minimization methods for functions depending strongly on a few variables; Conjugate gradients, method of). The choice of the step of the difference method and of the quantity
is a minimum point of it. Thus, the method of the heavy sphere is a particular case of the adjustment method. For the numerical solution of (1), or (2), one may, use, e.g., difference methods. In dependence on the choice of this difference method, discrete analogues of the method of the heavy sphere are obtained, including those for functions depending strongly on a few variables, the conjugate-gradient method, etc. (cf. Minimization methods for functions depending strongly on a few variables; Conjugate gradients, method of). The choice of the step of the difference method and of the quantity  strongly influences the rate of convergence of the method of the heavy sphere. Instead of (1), (2) other first- or second-order systems may be used (cf. [1]). In the problem of minimizing a function
strongly influences the rate of convergence of the method of the heavy sphere. Instead of (1), (2) other first- or second-order systems may be used (cf. [1]). In the problem of minimizing a function 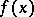 under the restrictions
under the restrictions
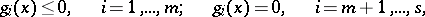 |
the method of the heavy sphere is applied in combination with the method of penalty functions, Lagrange functions, etc. (cf. [2], [3], Penalty functions, method of; Lagrange function).
References
| [1] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [2] | F.P. Vasil'ev, "Numerical methods for solving extremum problems" , Moscow (1980) (In Russian) |
| [3] | Yu.G. Evtushenko, "Numerical optimization techniques" , Optim. Software (1985) (Translated from Russian) |
Heavy sphere, method of the. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Heavy_sphere,_method_of_the&oldid=14643